[알고리즘] 탐색 BFS, DFS _ 백준 1260 파이썬
○ 탐색 알고리즘
코딩테스트 단골 문제 BFS, DFS
흔히 BFS, DFS + 재귀 문제만 잘 풀어도 코딩테스트에 통과할 수 있다고 하는데요. 그만큼 단골문제로 등장하는 BFS(너비 우선 탐색), DFS(깊이 우선 탐색)에 대해 알아보고 관련 백준 예제도 풀어도보도록 하겠습니다.
우선 탐색 이란 무엇인가.
프로그래밍을 할 때 데이터베이스 안의 수 많은 자료에서 원하는 자료를 찾으려면 어떻게 해야할까요?
만약 데이터가 정렬이 되어있다면 이진탐색을 통해서 최대 로그N의 연산만으로 찾을 수 있겠지만, 정렬이나 분류가 되어있지 않는 자료라면 이야기가 달라집니다.
원하는 자료를 찾을 때 까지 하나씩 직접 확인하며 찾아야합니다. 이러한 무식한 방법이 바로 깊이 우선 탐색(DFS)와 너비 우선 탐색(BFS) 입니다!
DFS, BFS 모두 탐색을 어떤 순서로 하느냐만 달를 뿐, 어떤 효율성도 생각하지 않고 모든 자료를 하나씩 확인해 본다는 점은 같습니다. 사실 코딩테스트에 많이 사용하는 알고리즘 이지만, 실제론 쓰이지는 않는다고 합니다.
이런 탐색이 또 쓰이는 곳은 바로 '게임'. 경우의 수들을 모두 확인하고 어떤 것이 최적인지 알아내기 위해 '탐색'이 사용된다고 합니다. 우리가 잘 아는 알파고에 쓰인 알고리즘 중 몬테카를로 트리 탐색 알고리즘이 있다고 합니다!

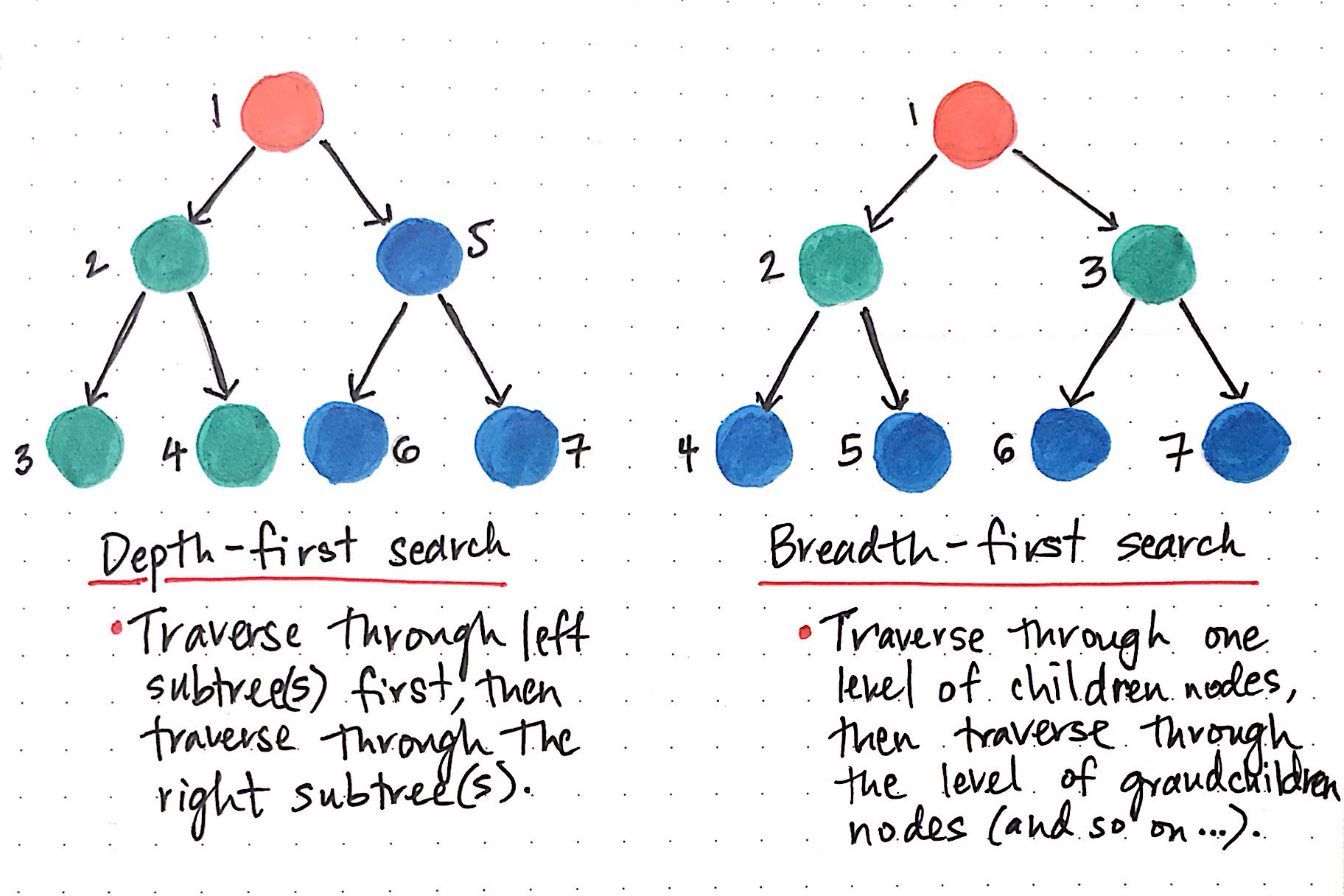
1. 너비 우선 탐색 (BFS : Breath First Search)

BFS는 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법입니다. BFS는 먼저 저장된 데이터를 꺼내서 쓰는 자료구조인 큐(queue)를 사용합니다.

한 단계 진행 시 가능한 경우의 수, 두 단계 진행 시 가능한 경우의 수 ... 이렇게 트리를 넓히면서 탐색하는 알고리즘이 바로 BFS 입니다.

수도코드
|
1
2
3
4
5
|
create a queue Q
mark v as visited and put v into Q
while Q is non-empty
remove the head u of Q
mark and enqueue all (unvisited) neighbours of u
|
cs |
예시

장점
- 답이 되는 경로가 여러개인 경우에도 최단 경로 보장
- 최단 경로가 존재하면 깊이가 무한정 깊어도 답을 찾을 수 있다
단점
- 경로가 길 경우 많은 기억 공간 필요
- 해가 존재하지 않는 유한 그래프의 경우 모든 그래프를 탐색 후 실패로 끝난다.
- 무한 그래프의 경우 해를 찾지도 끝내지도 못한다.
2. 깊이 우선 탐색 (DFS : Depth First Search)
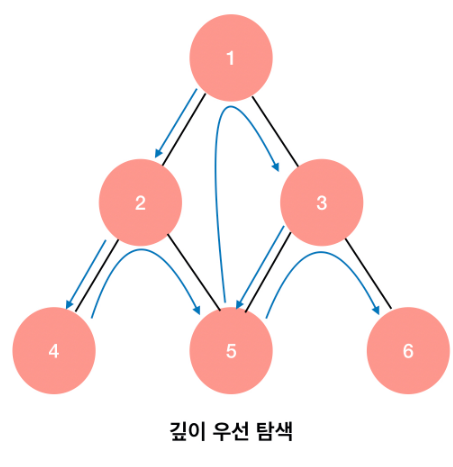
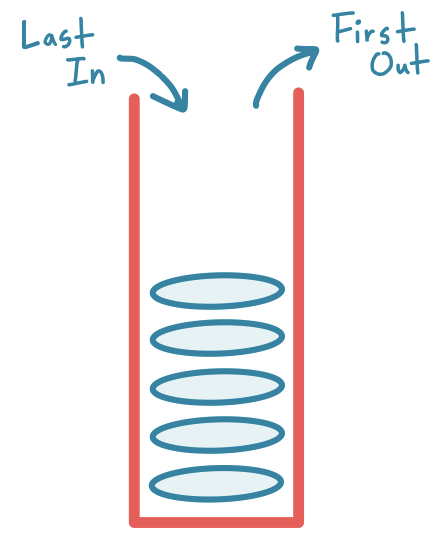
DFS는 하나의 정점에서 시작하여 그 정점의 인접한 정점 중 아직 방문하지 않은 정점이 없다면 탐색을 종료하고 있다면 방문하여 그 정점으로 부터 다시 DFS를 진행하는 재귀적인 방법으로 탐색하는 방법이며, 나중에 들어간 자료가 먼저 빠져나가는(Last In Fisrt Out) 스택(Stack)을 사용합니다.
DFS는 BFS와 다르가 여러 경우의 수 중 하나를 선택하고, 선택한 상황에서 가능한 여러 경우의 수 중 또 하나를 선택하며 트리의 깊이를 넓히며 탐색하는 방법입니다.
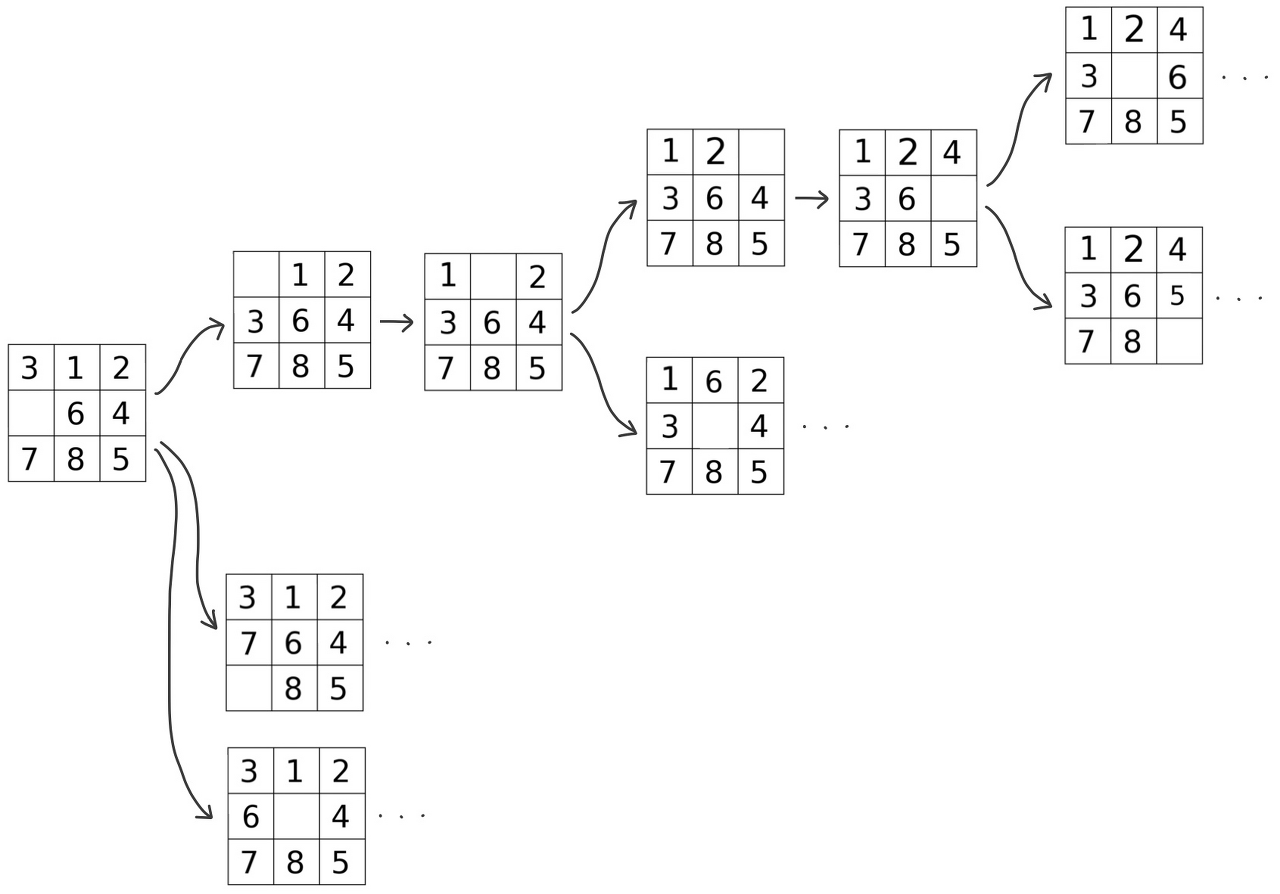
STEP
- 스택에 시작 노드를 넣는다.
- 스택이 비어있으면 실행을 멈추고 False 반환.
- 스택의 맨 위 노드가 찾고자 하는 노드라면 탐색을 종료하고 True 반환.
- 3.번에서 스택의 맨 위 노드가 찾고자하는 노드가 아니라면 해당 노드를 Pop하고, 스택에 들어온 적 없는 Pop한 노드의 모든 이웃 노드를 찾아 순서대로 스택에 Push
- 3.으로 돌아간다.
수도코드
|
1
2
3
4
5
6
7
8
9
10
11
|
DFS(G, u)
u.visited = true
for each v ∈ G.Adj[u]
if v.visited == false
DFS(G,v)
init()
For each u ∈ G
u.visited = false
For each u ∈ G
DFS(G, u)
|
cs |
DFS는 재귀 부분과 초기화, 실행 부분을 따로 만들어주는 것이 중요합니다.
예시
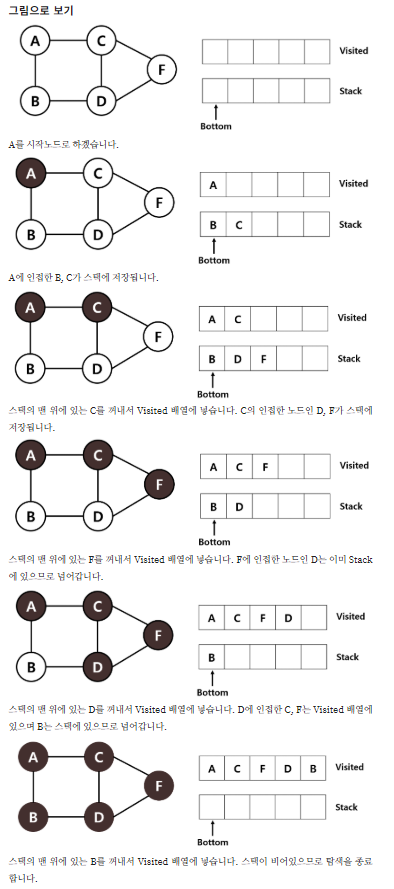
장점
- 현 경로상의 노드를 기억하기 때문에 적은 메모리를 사용
- 찾으려는 노드가 깊은 단계에 있는 경우 BFS보다 빠르다.
단점
- 해가 없는 경로를 탐색 할 경우 단계가 끝날 때까지 탐색한다.
- DFS는 해에 도착하면 탐색을 종료하기 때문에 최단경로라는 보장이 없다.
BFS, DFS 예제 : 백준 1260
문제
그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.
입력
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.
출력
첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다. V부터 방문된 점을 순서대로 출력하면 된다.
파이썬 코드
방법1_인접행렬로 그래프 구현
def dfs(v):
print(v, end=' ')
visit[v] = 1
for i in range(1, n + 1):
if visit[i] == 0 and s[v][i] == 1:
dfs(i)
def bfs(v):
queue = [v]
visit[v] = 0
while(queue):
v = queue[0]
print(v, end=' ')
del queue[0]
for i in range(1, n + 1):
if visit[i] == 1 and s[v][i] == 1:
queue.append(i)
visit[i] = 0
n, m, v = map(int, input().split())
s = [[0] * (n + 1) for i in range(n + 1)]
visit = [0 for i in range(n + 1)]
for i in range(m):
x, y = map(int, input().split())
s[x][y] = 1
s[y][x] = 1
dfs(v)
print()
bfs(v)
이렇게 인접행렬 방식으로 그래프를 만들어서 풀 때보다,
인접리스트로 그래프를 구현하니 훨씬 시간이 빨라졌습니다.
방법2_인접리스트로 그래프 구현
import sys
input = sys.stdin.readline
from collections import deque
def dfs(graph, v):
visited = []
stack = [v]
while stack:
n = stack.pop()
if n not in visited:
visited.append(n)
stack += reversed(graph[n])
return visited
def bfs(graph, v):
visited = []
queue = deque([v])
while queue:
n = queue.popleft()
if n not in visited:
visited.append(n)
queue += graph[n]
return visited
n, m, v = map(int, input().split())
graph = {i:[] for i in range(1,n+1)}
for i in range(1, m+1):
x, y = map(int, input().split())
graph[x].append(y)
graph[y].append(x)
for key in graph:
graph[key].sort()
print(' '.join(list(map(str,dfs(graph, v)))))
print(' '.join(list(map(str,bfs(graph, v)))))계속 런타임 에러가 나서 고생했는데 ㅜㅜ
고생한 이유1.
시작노드가 어느 간선과도 연결되지 않았을경우를 고려 X 때문
처음 그래프를 초기화 할 때 입력값으로만 그래프를 만들면 안되고,
graph = {i:[] for i in range(1,n+1)} 로 모든 노드를 키값으로 초기화 해놔야 한다.
그래야 연결된 간선이 없는 노드를 만났을 때 while queue나 while stack문을 빠져나갈 수 있기 때문.
고생한 이유2.
dfs시 그래프의 밸류값(노드에 연결된 childe 노드)를 역순 정렬해주어야 한다.
난이도 1개 짜리 맞는지.. 애매한 부분이 쫌 있었다.
그리고 if n not in visited 부분의 시간은 O(N)이다. visited를 리스트로 구현했기 때문에 리스트의 요소를 탐색하는데 총 N번의 시간이 소요되기 때문이다. 그래서 visited를 딕셔너리로 구현했더니 시간이 매우 줄었습니다.
방법3_visited={} 사용
import sys
input = sys.stdin.readline
from collections import deque
def dfs(graph, v):
visited = {}
stack = [v]
while stack:
n = stack.pop()
if n not in visited:
visited.setdefault(n)
stack += reversed(graph[n])
return visited
def bfs(graph, v):
visited = {}
queue = deque([v])
while queue:
n = queue.popleft()
if n not in visited:
visited.setdefault(n)
queue += graph[n]
return visited
n, m, v = map(int, input().split())
graph = {i:[] for i in range(1,n+1)}
for i in range(1, m+1):
x, y = map(int, input().split())
graph[x].append(y)
graph[y].append(x)
for key in graph:
graph[key].sort()
print(' '.join(list(map(str,dfs(graph, v)))))
print(' '.join(list(map(str,bfs(graph, v)))))
DFS BSF 관련 백준 문제
| No. | 난이도 | 백준 링크 |
| 1 | 🌕🌑🌑🌑🌑 | DFS와 BFS |
| 2 | 🌕🌗🌑🌑🌑 | 미로 탐색 |
| 3 | 🌕🌗🌑🌑🌑 | 숨바꼭질 |
| 4 | 🌕🌗🌑🌑🌑 | 유기농 배추 |
| 5 | 🌕🌗🌑🌑🌑 | 연결 요소의 개수 |
| 6 | 🌕🌗🌑🌑🌑 | 단지번호붙이기 |
| 7 | 🌕🌗🌑🌑🌑 | 로또 |
| 8 | 🌕🌕🌗🌑🌑 | 토마토 |
| 9 | 🌕🌕🌕🌑🌑 | 나이트의 이동 |
References