Sampling Distribution

빅데이터가 많아짐에 따라 표본 추출(sampling)이 필요 없는 것은 아니다.
데이터의 질과 적합성을 일정 수준 이상으로 담보할 수 없는 데이터가 훨씬 많을 뿐더러 다양한 데이터를 효과적으로 다루고 데이터 편향을 최소화하기 위해 표본추출의 중요성이 더 커지고 있다. 또, 모델링의 경우 결국 작은 sample data를 가지고 예측 모델을 개발하고 테스트하기도 한다.

 

Sampling Distribution (표본 분포)

 

Ramdom Sampling and Sample Bias

• Ramdom Sampling

모집단 내에서 무작위로 샘플을 추출하는 경우로 그 결과 얻은 데이터를 Simple ramdom sample(단순임의표본)이라고 한다.
중복 추출이 가능하도록 추출한 샘플을 다시 모집단에 포함시키는 것을 복원 추출(with replacement)
한번 뽑은 샘플은 추후 샘플링에 사용하지 않는 것을 비복원 추출(without replacement)라고 한다.

 

데이터가 품질이 좋다는 것은 데이터의 완결성, 형식의 일관성, 깨끗함 및 값의 정확성을 가지고 있다는 것을 의미한다.
그리고 또 중요한 것이 바로 '대표성(representativeness)'이다.
sample은 population을 대표할 수 있어야 한다. 완전한 random이 아닌 nonrandom하게 뽑힌 샘플은 모집단을 정확하게 대표할 수 없게 된다. 따라서 대표성을 담보하기 위해서는 정확한 ramdom sampling이 중요하다.

 

• stratified sampling(층화표본추출) : 모집단을 층으로 나눠 각 층에서 ramdom sampling 하는 것. (ex. 여성 그룹, 남성 그룹)

 

• Sample Bias

population과 sample 사이의 차이가 유의미할만큼 크고 첫 번째 표본과 동일한 방식으로 추출된 다른 샘플들에서도 이 차이가 계속될 것으로 예상된다면 sample bias가 발생했다고 볼 수 있다.

 

• bias : 통계적 bias는 측정 과정 혹은 sampling에서 발생하는 계통적인(syntematic) 오차를 의미한다.

 

ramdom sampling으로 인하나 오류와 편향에 따른 오류는 신중하게 구분해야 한다.
bias가 없는 프로세스에도 오차가 있기는 하지만 이는 눈으로 보기에도 데이터 분포가 랜덤하며 어느 한쪽으로 치우치지 않는다.

 

 

When we need Big data

대량의 데이터가 필요한 경우는 데이터가 크고 동시에 희소할 때이다. 그리고 데이터가 축적될수록 결과가 더 좋은 경우이다.

 

 

---

Selection Bias

• selectio Bias : 관측 데이터를 선택하는 방식 때문에 생기는 편향
• Data Snooping : 흥미로운 것을 찾아 데이터를 광범위하게 살피는 것
• Vast Search effect : 중복 데이터 모델링이나 너무 많은 예측 변수를 고려하는 모델링에서 비록되는 편향 또는 비재현성

데이터를 광범위하게 살피거나 큰 데이터 집합을 가지고 반복적으로 다른 모델을 만들 경우 언젠간 흥미로운 결과를 발견하기 마련이다.
그 결과가 정말로 의미 있는것인지 우연인것인지 잘 판단해야 한다.
이를 방지하기 위해 두개 이상의 holdout 세트를 이용하거나 target shuffling을 이용할 수 있다.
또 nonramdom sampling, data cherry picking, time interval selection, 결과가 만족스러우면 실험 멈추기 등은 문제를 초래할 수 있다고 한다.

 

Regression to the mean

평균으로 회귀란, 어떤 변수를 연속적으로 측정했을 때 나타나는 현상이다. 예외적인 경우가 나타나면 그 다음에는 중간정도 경우가 나타나는 경향을 말한다. 여기서의 회귀는 선형 회귀의 회귀와 다름.

 

---

Sampling Distribution

뽑는 표본에 따라 모델링하는 결과가 달라질 수 있으므로 표본의 변동성(sample variablility)를 관찰해야 한다.

 

• Sample statistic : population에서 추출된 sample들로부터 얻은 측정 지표
• Data distribution : 데이터 집합에서의 각 개별 값의 도수분포

평균과 같은 표본통계량의 분포는, 데이터 자체의 분포보다 규칙적이고 종모양(gaussian(=normal) distribution) 형태이 확률이 높으모 표본이 클수록 그 확률은 더 높다. 그리고 표본이 클 수록 표본통계량의 분포가 좁아진다.

 

• Sampling distribution : 여러 표본들 혹은 재표본들로 부터 얻은 표본통계량의 도수분포
  모집단으로부터 표본 추출을 반복시행하여 추출할 수 있는 모든 가지 수의 표본을 추출했다면, 추출된 표본가지 수 만큼의 통계량이 존재하게 된다. 이들의 통계량에 대한 분포를 sampling distribution이라고 한다.

 

• Central limit theorem(중심극한정리) : 표본크기가 커질수록 표본분포가 정규분포를 따르는 경향
  central limit theorem은 모집단이 정규분포가 아니더라도, 표본의 크기가 충분하고 데이터가 정규성을 크게 이탈하지 않는 경우 여러 표본에서 추출한 평균은 종모양의 정규곡선을 따른다는 것이다. central limit theorem 덕분에 추론을 위한 표본 분포에, 신뢰구간이나 가설검정을 하는데 t분포 같은 정규근사 공식을 사용할 수 있다.

 

• Standard error(표준오차) : 표본의 표준편차 (표준편차는 개별 데이터의 값의 변량)

표준 오차는 표본 분포의 variability를 한마디로 설명해주는 단일 측정 지표이다.
표준 편차 s와 표본크기 n을 기반으로 한 통계량을 이용해 추정한다.
표준 오차와 표본 크기는 n제곱근 법칙에 따라 표준 오차를 2배로 줄이려면 표본 크기를 4배로 증가시켜야 한다.

 

• Standrad error of Mean(SEM, 평균의 표준오차) : 표본 평균의 표준 오차

100 번 표본을 추출해보고 그 때 마다 얻게되는 표본 평균을 그린 것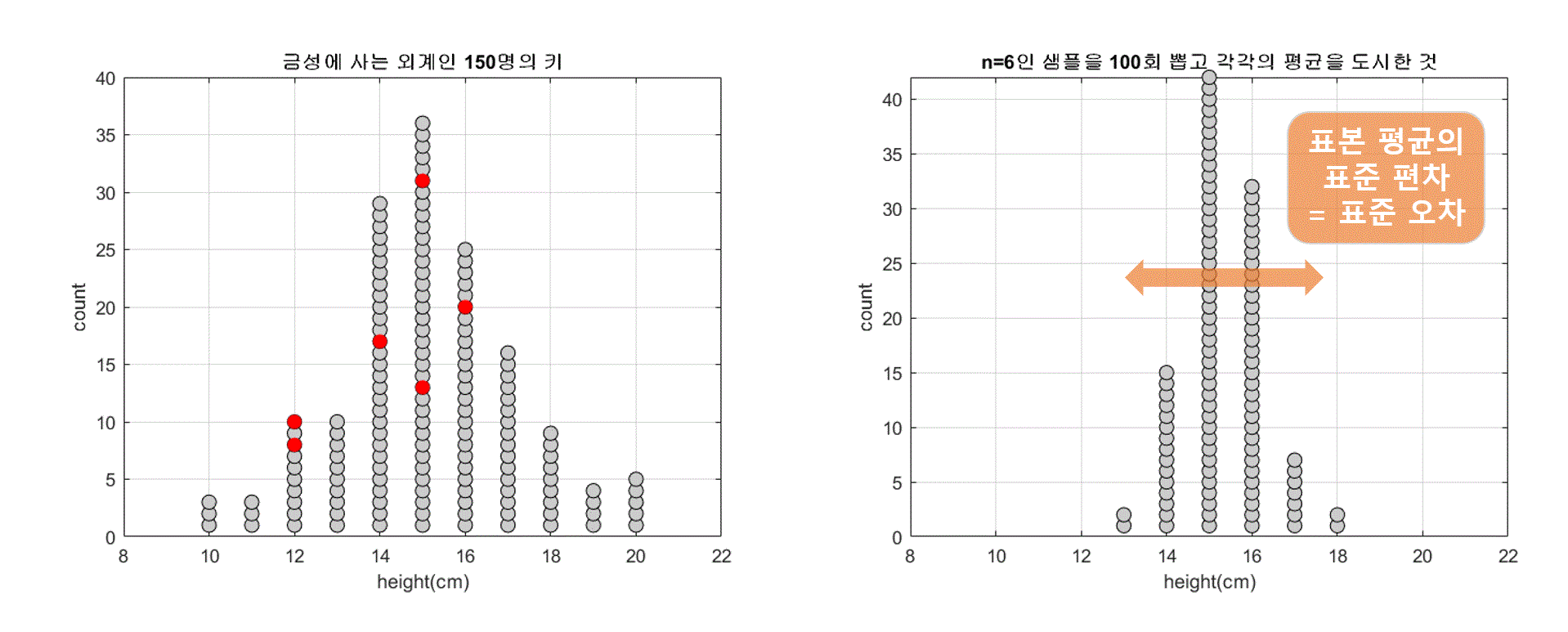

위 그림  출처  최종 그림

위 그림 출처

 

 

---

** 모분산의 기호 : 시그마, 샘플 분산의 기호 : s
** 모평균의 기호 : 뮤, 샘플 평균의 기호 : x바
** 모수(parameters) : population의 특성 (평균, 분산, 표준편차 ...)
** 통계량 : population에서 추출한 sample을 이용해 만든 sample들의 함수 (표본평균, 표본분산)

** sample mena(표본평균), ample distributuion(표본분산) : n개의 random sampling해서 얻은 샘플의 평균. 표본 평균을 새로운 확률변수라고 생각하고 표본평균의 평균과 분산을 구할 수 있음.

예를 들어서 남성의 평균 키를 구하려고할 때 지역별 평균 남성의 키에 대한 샘플이 있다고 해보자. 그러면 지역별 평균키 값을 이용해서 평균과 분산을 구할 수 있다. 즉, 지역별 평균키를 새로운 확률변수로 생각하는 것이다. 이것을 sampling distribution of the mean이라고 하며 회귀분석에서 중요한 개념으로 사용된다.

---

 

Bootstrap

통계량이나 모수(parameters)의 표본분포를 추정하는 쉽고 효과적인 방법으로, 현재 있는 표본에서 추가적으로 표본을 복원 추출하고 각 표본에 대한 통계량과 모델을 다시 계산 하는 것. 표본통계량이 정규분포를 따라야 한다는 가정은 꼭 필요하지 X
반복 횟수가 많을 수록 표준오차나 신뢰구간에 대한 추정이 더 정확해진다.
sample 크기가 작은 것을 보완하기 위한다거나 새 데이터를 만드는 것이 X 단지 표본이 얼마나 원래 표본과 비슷할지 알려줄 뿐.

R에서는 boot 함수를 제공하고, 파이썬에서는 sklearn의 resample 함수를 이용할 수 있다.

부트스트랩은 다변량 변수의 경우에도 이용할 수 있다. 각 행은 여러 변수들의 값을 포함하는 하나의 샘플을 의미한다. 모델 파라미터의 안정성(변동성)을 추정하거나 예측력을 높이기 위해 부트스트랩 데이터를 가지고 모델을 돌려볼 수 있다. 

분류, 회귀 트리(의사결정트리)를 사용할 때, 여러 부트스트랩 샘플을 가지고 트리를 여러개 만든다음 각 트리에서 나온 예측 값을 평균 내는 것이 단일 트리를 사용하는 것보다 효과적이다.(emsemble의 bagging)

 

• bootstrap sample : 관측 데이터 집합으로부터 얻은 복원추출 표본
• resampling : 관측 데이터로부터 반복해서 표본추출하는 과정. 부트스트랩과 순열(shuffling) 과정 포함

 

 

Confidence Interval

freqency table, histogram, boxplot, standard error는 모두 sample estimate에서 잠재적인 오차를 이해하는 방법인데, '신뢰구간'은 이와 다르다.

• Interval(신뢰구간) : 구간 범위로 추정값을 표시하는 방법
• Confidence level(신뢰수준) : 같은 모집단으로부터 같은 방식으로 얻은 관심 통계량을 포함할 것으로 예상되는 신뢰구간의 백분율
  포본 추정치 주의의 x% 신뢰구간이란, 평균적으로 유사한 표본추정치 x% 정도가 포함되어야 한다.
  90% 신뢰구간이란, 표본통계량의 부트스트랩 표본분포의 90%를 포함하는 구간을 말한다.
  잠재 오류를 알려주거나 더 큰 표본이 필요한지 여부를 파악하는 용도로 사용한다.
  신뢰수준이 높을수록 구간이 더 넓어지며 표본이 작을수록 구간이 넓어진다.(불확실성이 커진다.)

 

• confidence interval을 구하는 법

1. 데이터를 복원추출 방식으로 sampling한다.
2. resample에 대해 원하는 통계량을 기록한다.
3. 1-2단계를 R번 반복한다
4. x% 신뢰구간을 구하기 위해 R개의 재표본 결과의 분포 양쪽 끝에서 [(100-x)/2]%만큼 잘라낸다.
5. 절단한 점들은 x% 부트스트랩 신뢰구간의 양 끝점이다.

 

 

부트스트랩은 대부분의 통계량 혹은 모델 파라미터에 대한 신뢰구간을 생성하는데 사용할 수 있는 일반적인 방법이다.

 

Expectation / Mean / Average

예를 들어 주사위를 5번 던졌다고 해보자. 5번의 결과가 2,4,5,1,2가 나왔다면 주사위를 던져서 나오는 숫자의 Mean은 2.8이 된다.
위 문제에서 Expectation은 1*1/6 + 2*1/6 + 3*1/6 + 4*1/6 + 5*1/6 + 6*1/6 = 3.5가 된다.
즉, Mean은 Sample에 Dependent 하며 Expectation는 랜덤 변수가 주어졌을 때 기대하는 값을 말하게 된다.
샘플이 무한정 커진다면 mean은 expecation에 근사하게 되며 Mean=Expecation이 된다.
Average는 Mean의 한 종류라고 보면 된다. 우리가 일반적으로 Mean을 구한다고 할 때 사용하는 공식(모든변수의합/변수의갯수)은 Arithmetic Mean을 말하고 이 외에도 Harmonic Mean 등의 종류가 있다.

 

 

variance, correlation coefficient에서 분모가 n이 아닌 n-1인 이유는?

일단 여기서의 variance는 표본분산을 의미하며 모분산이 X

분산 수식(모분산)

표본 분산 수식

총 세가지 관점에서 이를 설명할 수 있다.

1. sample variance를 unbiased estimator하게 만들기 위해서

통계에서 Population의 통계량(모수=parameters)를 알 수 없기 때문에 표본의 통계량을 통해 Population의 통계량을 추정하게 된다. 이렇게 추정하는 값을 '추정량(estimate)'라고 하며 표본평균, 표본 분산도 추정량에 해당한다. Unbiased estimate란, expected value가 parameters와 동일한 estimate라는 뜻이 된다.
표본 평균은 그 값이 모집단에서 치우쳐진 값이라고 하여도 계속해서 샘플을 랜덤으로 추출하면 샘플 평균은 모평균에 수렴하게 된다. (예를 들어서 모집단이 1,2,3,...8,9 이라고 하고 sample을 3개를 추출한다고 할 때 1,2,3가 추출되었다면 평균은 2로 모평균과 거리가 있지만 다음 샘플에서 7,8,9가 뽑혔다면 차이가 어느정도 해결될 것이다.)
하지만 샘플 분산의 경우 치우친 샘플이 뽑혔을 경우 모평균 기준에서 분산 기여도가 높지만 샘플 평균 기준에서는 작기 때문에 underestimate가 누적되게 되어 모분산에 수렴하지 않게 된다. 때문에 분모를 n-1로 해주어 underestimate를 보정해주는 것이다.

 

2. 왜 n-1인지? 자유도 관점

n-2일 수도 있고 n-3일수도 있다. 하지만 왜 n-1을 굳이 샘플 분산의 분모로 취해주게 되는지는 '자유도(degree of freedom)'라는 개념 때문이다. 자유도는 독립변수의 갯수를 의미한다.(예. x+y+z=3이 있을 때 x와 y를 알면 z를 알 수 있기 때문에 z는 종속변수이며 따라서 자유도는 2이다.) 3개의 샘플 평균이 5라면 2개만 뽑아도 나머지 숫자가 정해진다. 샘플 분산을 구하기 위해서 샘플 평균을 구했기 때문에 우리가 자유롭게 정할 수 있는 값은 2가 되는 것이다.

 

3. 수학적으로 샘플 분산의 분모가 n-1이면 샘플 분산의 기대치를 구하면 모집단의 분산과 같아지기 때문(아래 링크 참고)
   (참고한 글 : 링크)

 

---

 

 

Normal distributuion(=Gaussian distributuion)

정규 분포가 중요한 이유는 표본 통계량 분포가 보통 일정한 어떤 모양(정규분포)이 있다는 사실이다. 그리고 특히 이 분포를 근사화하는 수학 공식을 개발하는데 강력한 도구가 되었다는 점에 의의가 있다. 즉, 정규 분포는 불확실성과 변동성에 관한 수학적 근거를 가능하도록 했다. 그렇다고 원시 데이터 자체가 정규분포를 따른다는 것은 아니고(데이터는 일반적으로 정규분포르 따르지 않는다.), sample들의 평균, 합계, 오차는 많은 경우 정규분포를 따른다는 점이 유용하다. 

• error(오차) : 데이터 포인트와 예측값 혹은 평균 사이의 차이
• standardize : 평균을 빼고 표준편차로 나눈다.
• z-score : 개별 데이터 포인트를 정규화한 결과
• standard normal distributuion : 평균 0 표준편차 1인 정규분포
• QQ-plot : 표본 분포가 특정 분포(ex. 정규분포)에 얼마나 가까운지 보여주는 그림
  대부분의 원시데이터가 정규분포를 따르진 않지만 표본분포에서 대부분의 통계량이 정규분포를 따른다는 점에서 정규분포의 유용함이 드러날뿐이다. 표본들의 평균과 합계, 오차는 많은 경우 정규분포를 따른다.
  정규분포는 불확실성과 변동성에 관한 수학적 근사가 가능하도록 했다.

 

Chi-square distributuion

Chi, 카이( χ )는 평균0 분산1인 표준정규분포를 의미한다. 따라서 카이제곱은 표준정규분포를 제곱한다는 의미가 내포되어 있다.
평균(데이터의 중심위치)을 기준으로 데이터가 흩어져 있는 정도(치우침의 척도)를 나타내는 분산. 바로 그 분산의 특징을 확률분포로 만든 것이 카이제곱분포이다.

집단의 분산을 추정하고 검정할 때 많이 사용하며 분산을 다루고 있기 때문에 음이 없고 +만 있어 비대칭 모양을 띄고있다.

그리고 보통의 경우 평균과 가까운 값이 많지 한쪽으로 치우쳐진 경우는 별로 없다.

때문에 0의 오른쪽 부분에 분포가 많고(치우침이 많지 않은 경우)

0에서 멀어질 수록 분포가 적다.(치우침이 매우 큰 경우)

카이제곱 통계는 귀무 모델(모든 그룹의 평균이 동일한 경우)의 기댓값에서 벗어난 정도를 측정한다.

 

 

T-distributuion

자유도v에 따라 모양이 달라짐

student의 t-distributuion은 normal distribution과 생김새가 비슷하지만 꼬리가 약간 더 두껍고 긴 모양을 하고 있다.
t분포는 표본통계량의 분포를 설명하는데 광범위하게 사용되며 표본평균의 분포는 일반적으로 t분포 모양이다.
표본이 클수록 더 정규분포를 닮은 t분포가 형성된다. 보통 표본수가 30이하일 때는 정규분포대신 t-분포를 사용하게된다.

이유는 표본의 크기가 작으면 신뢰도가 낮아지기 때문에 예측범위가 좀 더 높은 t-분포를 사용하는 것이다.

표본평균, 두 표본평균 사이의 차이, 가설검정, 회귀 파라미터 등의 분포를 위한 기준으로 널리 사용된다.

 

F-distributuion

F분포는 정규분포를 이루는 모집단에서 독립적으로 추출한 표본들의 "분산 비율"이 나타내는 연속확률분포이다.

F분포는 카이제곱과 마찬가지로 '분산'을 다루지만, 카이제곱은 한 집단의 분산을 다루며 F분포는 두 집단의 분산을 다룬다.
F분포는 측정된 데이터와 관련한 실험 및 선형 모델에 사용되며 두 가지 이상의 표본집단과 분산을 비교하거나 모집단의 분산을 추정할 때 쓰인다.

 

=> F분포, T분포, 카이제곱분포는 확률을 구할 때 사용하는 것 X 신뢰구간과 가설검정에서 사용하는 분포이다.

 

Poisson distributuion

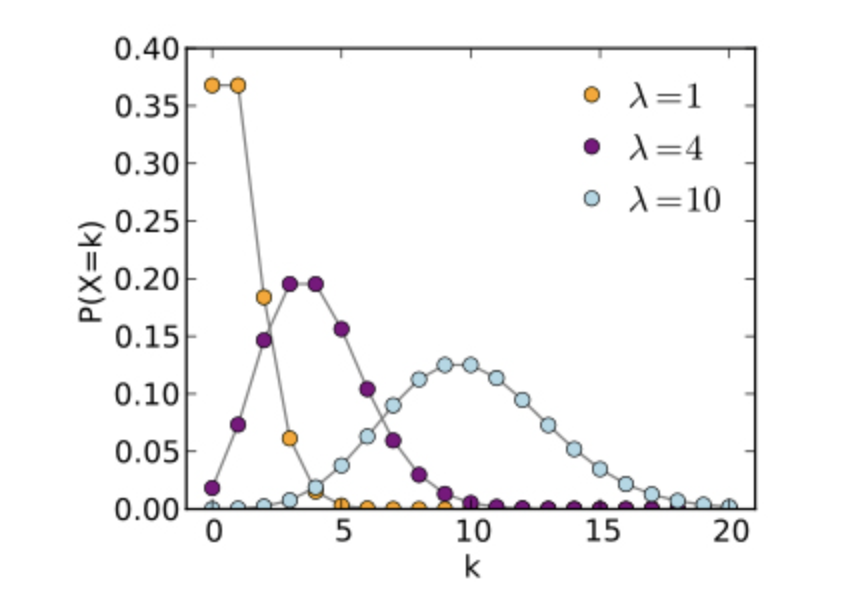
• lambda : 단위 시간이나 단위 면적당 사건이 발생하는 비율. 기댓값과 분산이된다.
• Poisson distribituion(푸아송분포) : 표집된 단위 시간 혹은 단위 공간에서 발생한 사건의 도수분포이며 이산 확률분포에 속한다.

푸아송 분포에서 확률은 모수에 따라 결과가 달라진다.

푸아송 분포의 전제조건은 독립성, 일정성, 비집락성이 있다. 비집락성이란 짧은 시간이나 공간에서 두 개 이상의 결과가 동시에 발생할 확률은 0이라는 뜻이다. (ex. 9-10시에 은행에 들른 고객수와 10-11시에 은행에 들른 고객수는 독립적이다. 같은 지점에 같은 시간에 교통사고가 두 번 이상 발생할 확률은 무시해도 좋다.)

 

Long-tailed Distribution

• tail : 적은 수의 극단값이 주로 존재하는 frequency distributuion의 길고 좁은 부분
• skewness(왜도) : 분포의 한쪽 꼬리가 반대쪽 다른 꼬리보다 긴 정도
  **관측된 자료에 적합한 통계분포를 찾는 것은 데이터만 판단하는 것보다 좋을 수 있다. 예를 들어 푸아송 분포는 시간 주기별 이벤트를 모델링하는데 가장 적합한 분포이다.

 

Binomial Distributuion

• trial : 독립된 결과를 가져오는 하나의 사건
• binomial(이항식) : 두가지 결과를 갖는다.
• binominal distributuion(이항분포) : n번 시행에서 성공한 횟수에 대한 분포

이항분포란 각 시행마다 성공확률 p가 정해져 있을 때 주어진 시행 횟수 n 중에서 성공한 횟수 x의 frequency distributuion을 말한다.
n과 p에 따라 다양한 이항분포가 있다. 이항분포의 평균은 n*p이며 분산은 n*p(1-p)이다.

이항 분포에 극한을 취하면, 푸아송 분포가 된다.
시행횟수가 클수록 사실상 정규분포와 구분이 어려워 대부분 통계절차에서는 평균과 분산으로 근사화한 정규분포를 사용한다.
ex. 한 번의 클릭이 판매로 이어질 p가 0.02일 때, 200번 클릭으로 0회 매출을 관찰할 확률은 얼마인가?

 

 

그 외 분포.. Exponential distributuion, Weibull distributuion