KL-Divergence
Entropy
Entropy는 정보를 표현하는데 있어 필요한 평균 최소 정보 자원량을 말한다.
그래서 Entropy가 크면 나타내는 정보량이 많다는 것을 의미한다.
예를 들어서 "월화수목금토일" 7개 요일을 표현한다고 하면, 총 7bit가 필요할까?
월 000 화 001 수 010 목 100 금 101 토 110 일 011 이런식으로 정보를 인코딩해서 표현하게 되면 7개의 요일을 표기하는데 약 3bit가 필요하다. N개의 정보를 표시하는데 총 log_2(N) 비트가 필요하다. 즉, 최소 자원량은 bit로 얼마나 짧게 표현될 수 있느냐를 의미한다.

맑은날인지 비가 오는 날인지 정보를 표현한다고 할 때,
실제로 맑은날이 비오는날 보다 더 자주 있으므로 맑은날을 표현할 때 더 짧은 bit로 전송해야 할 것이다.
확률이 작을 수록 더 긴 bit로 표현해야 하므로 이를 그래프로 표현하면 위 그림과 같이 될 것이다. 여기서 log의 밑을 2로 표현한 것은 비트로 표현해야해서 그렇다.
월~일 까지의 요일을 전송한다고 할 때 각 요일의 발생할 확률은 uniform하다. 때문에 log_2(7) = 2.8 비트가 필요하다.
A,B,C,D,E,F,G 라는 7개의 문자를 전송한다고 가정하고 각 문자를 보내는 경우는 독립이라고 하자. 그런데 A,E 를 보내게될 확률이 80%고 나머지는 20%라고 해도 똑같이 logN bit가 필요할까?
맨 첫번째 비트를 A,E인지 구분하는 비트로 두면
A,E 표현 => 1 bit + log2 bit = 2 bit
B,C,D,F,G => 1 bit + log5 bit = 3.3 bit
가 필요한데 이때 평균적으로 필요한 bit수는 0.8*2 + 0.2*3.3 = 2.26 bit이다.
똑같은 문자 수인데 필요한 평균 자원량이 밑의 경우가 더 적다.
즉 정보량이란 것은 각 레이블이 발생할 확률을 고려하고, 최소 자원량인 entropy가 maximum할 때는 모든 정보의 확률이 uniform할 때이다.

확률변수 x의 Entropy를 나타내는 함수를 H(x)라고 하고 각 확률변수의 확률을 P(x)라고 하자
그리고 x는 맑은날, 흐린날 두가지의 경우를 가진다고 하자.
P(sunny) = 0.8, P(cloudy) = 0.2라고 할 때 위에서 설명했듯 P와 H는 monotonic한 관계를 가지므로,
일단 H(sunny) < H(cloudy) 일 것이다.
여기서 추가로 확률변수 y를 같이 표현한다고 해보자. y는 비옴, 안옴 두가지의 경우를 가지고 x와 y는 서로 독립이다.
H(x, y) = h(x) + h(y)
P(x, y) = p(x) * p(y)
그리고 entropy의 함수와 확률 함수의 관계를 나타내려고 할 때,
f(p(x, y)) = f(p(x)*p(y)) = f(p(x)) + f(p(y))를 만족하는 함수 f는 log함수가 된다. (logxy = logx + logy기 때문에 즉 log여야 독립일때 덧셈으로 표현이 가능)
확률이 커질 수록 H는 작아져야 하기 때문에 앞에 -가 붙어 H(x) = -log_2P(x)가 된다.
그리고 최소 자원량을 랜덤하게 보려면 결국 기댓값으로 표현해야 하기 때문에 위 그림의 수식이 최종 Entropy 식이 된다.
어떤 경우에도 Entropy 식보다 작게 정보를 표현할 수 없는 low bound이다.
그리고 이 Entropy를 가지고 무엇을 할 수 있냐. Uncertainty(불확실성)을 측정할 수 있다.
빨간 파랑공이 7:3으로 들어있는 주머니와 5:5로 들어있는 주머니 중 어떤 공이 더 자주 나올지 예측하기 쉬운쪽은 전자일 것이므로 불확실성이 낮다고 볼 수 있고 Entropy가 낮다고 볼 수 있다. 만약 주머니에 모두 빨간공만 들어있는 경우는 Entropy가 0이 될 것이다.
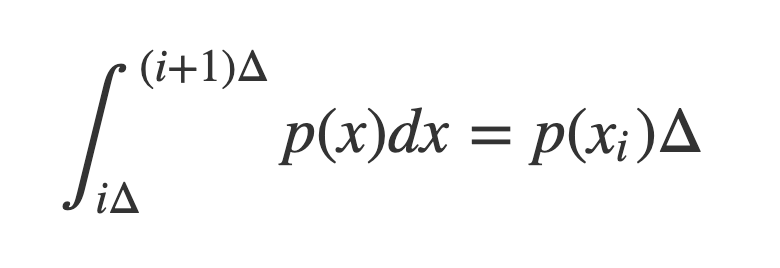
그리고 확률 변수가 Continuous 한 경우에는 Differencial Entropy를 정의할 수 있다. 평균값 정리에 의해서 위 식을 만족하는 value Xi를 반드시 찾을 수 있으므로,

Continuous 인 경우에 Entropy는 위 식과 같이 정의할 수 있다.

이때 limΔ -> 0을 취하게 되면 위와 같은 식이 얻어지게 된다.


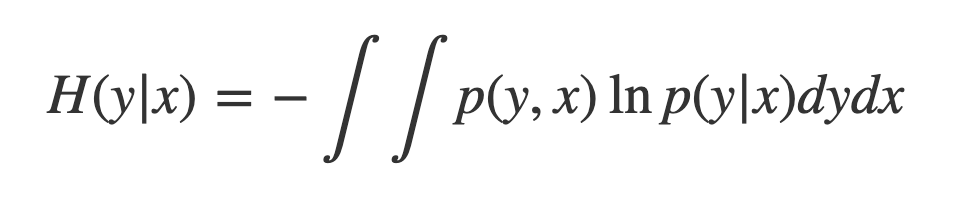
그리고 확률변수가 2개인 경우 joint distributuion P(x, y)에 대해 우리가 알고 있는 정보는 x라고 할 때 y의 information의 양을 계산하는 Conditional Entropy는 위 수식과 같다. 그리고 Chain Rule은 H(x, y) = H(y|x) + H(x)를 항상 만족한다.
Cross Entropy

Entropy 식에서 P(X)는 사건이 발생할 실제 확률을 말한다.
맑은날과 흐린날이 관측될 확률이 실제로 80%와 20%라면 Entropy이다. 하지만 내가 실제 확률을 모를 때 임의로 맑은날 흐린날이 발생할 확률을 동등하게 50% 50% 준다면 이 확률은 위 그림의 식에서 q(x)가 되는 것이다.
내가 임의로 uniform하게 확률을 주면 실제 Entropy보다 비효율적일 것이다. 때문에 Entropy보다 Cross Entropy가 더 큰 값을 가진다.
비효율적으로 잰 정보량 Cross Entropy와 진짜 찐 정보량 Entropy의 차이를 재는 것이 바로 KL Divergence이다.
KL-Divergence(쿨백 라이블러 발산)

KL-Divergence는 정보엔트로피에서 크로스엔트로피를 뺀 값이다. KL Divergence가 상대 엔트로피(Relative Entropy)라고도 불리는 이유다.
머신러닝에서 Cross Entropy의 Q(x)는 우리가 예측한 모델이 내놓은 확률을 말한다. 따라서 KL-divergence는 내가 만든 모델이 예측하는 것과 실제 결과의 차이라고 볼 수 있다. 더 정확하게 말하면 Q의 경우 가설, 모델, 모델이 예측한 값, 모델이 내논 분포나 결과 등등 P를 근사한 값을 말한다.
KL Divergence는 근사 모델(Q)를 실제 분포(P)와 가깝게 만들기 위한 목적 함수(objective function)로 사용하고 KL-divergence가 최소화 되도록 학습하게 된다. 그리고 머신러닝에서 learning하는 것은 Q이기 때문에 cost(loss)를 Cross Entropy로 잡으나 KL-divergence로 잡으나 동일하다.
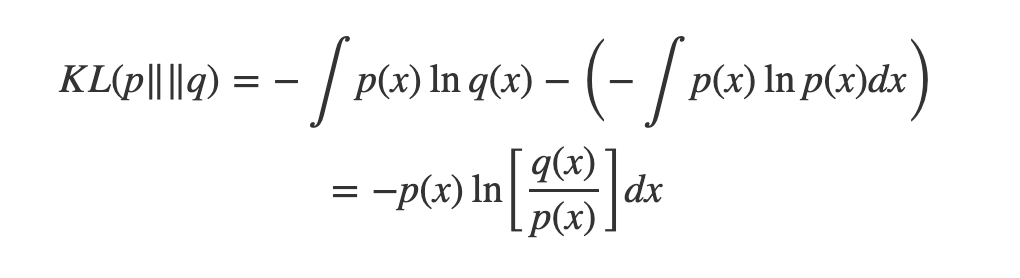
Continuous 인 경우는 위 식처럼 쓸 수 있다. Discrete한 예측 레이블이 아닌 Continuous한 Distribution을 비교하는 경우는 위와 같이쓴다.
그리고 KL Divergence의 큰 특징 두가지는
- 항상 0 이상의 값을 갖고
- 비대칭(Asymmetric)하며
- 두 확률 분포가 동일할 때 0이 된다
는 것이다.
KL Divergence는 직관적으로 두 분포의 거리라고 생각할 수 있지만 거리가 될 수 없다.
Distance라고 하면 Symmetic 해야 하는데 KL(P||Q) 와 KL(Q||P)는 같지 않다.
KL divergence는 언제나 0보다 크며 0이 되는 경우는 두 분포 P, Q가 같은 경우 뿐이라는 것은 Convexity 컨셉과 Jensen's Inequality를 도입해 증명이 가능하다.
Mutual Information
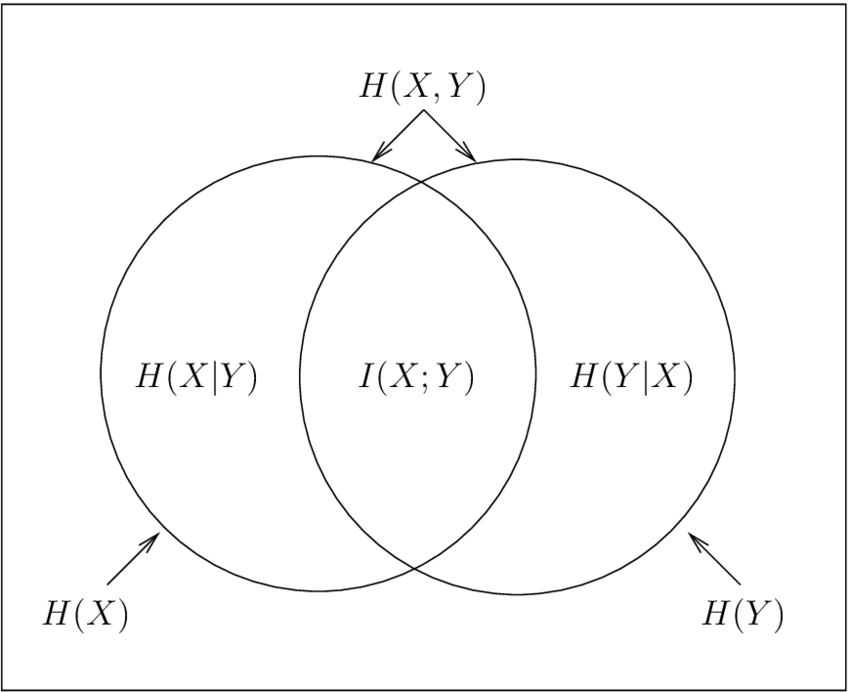
Mutual Infromation은 두 확률변수가 얼마나 서로 dependency한지 측정할 수 있는 척도이다. 두 확률변수가 얼마나 mutually(서로) dependent(독립) 인가 얼마나 mutually information을 많이 가지고 있는지 알 수 있다.

두 확률변수가 독립이라면 P(x,y) = p(x)p(y)가 될 것이고 logp(x,y)/p(x)p(y) = 1이 될 것이고 log 1 = 0이므로 Mutual Information I는 0이된다.
실제 독립이 아닌데 -> p(x,y)
독립인 것 처럼 생각했을 때 -> logp(x,y)/p(x)p(y)
를 곱한 것이다.
Mutual information을 Bayes perspective에서 바라보게 된다면, 만약 우리가 어떤 데이터 x의 prior p(x)를 관측하고, 새로운 데이터 y를 관측해 얻은 posterior distribution p(y|x)가 있다고 했을 때, Mutual information은 이전 관측 x를 통해 새로운 관측 y의 uncertainty가 얼마나 줄게 되는지 알 수 있다.
'인공지능 AI' 카테고리의 다른 글
| [CS25 1강] Transformers United: DL Models that have revolutionized NLP, CV, RL (0) | 2023.03.15 |
|---|---|
| [RL] Bayes-Adaptive Monte-Carlo Planning and Learning for Goal-Oriented Dialogues (0) | 2023.01.08 |
| Model-based Reinforcement Learning (0) | 2022.03.18 |
| MLE(Maximum Likelihood Estimation) 최대우도법 (0) | 2021.10.28 |
| Sampling Distribution (0) | 2021.05.06 |
소중한 공감 감사합니다