Encoding Recurrence Into Transformer, ICLR 2023

Encoding Recurrence Into Transformer

 

Link : https://openreview.net/pdf?id=7YfHla7IxBJ

 

 

Abstract

 

해당 논문은 RNN layer를 간단한 RNN의 sequence로 표현할 수 있음을 보이고, 이를 Transformer의 self-attention의 lightweight positional encoding matrix로 사용할 수 있음을 보인다. RNN layer에서 사용되는 recurrent dynamics는 multihead self-attention의 positional encoding으로 압축될 수 있고 이는 Transformer에서 recurrent dynamics를 통합할 수 있음을 의미한다. 여기서 소개되는 Reccurrence Encoding Matrix(REM)은 positional encoding matrix를 대체할 수 있으며, 이 matrix가 적용된 Self attention module은 Self-Attention with Recurrence(RSA)이며, 저자들이 소개하는 새로운 모듈이다. REM은 recurrent inductive bias를 내포하고 있으며 이를 사용하면 기존 트랜스포머는 non-recurrent sigmal 부분만 모델링하고 reccurent signal은 REM으로 모델링해서 기존의 트랜스포머보다 더 좋은 샘플 효율성을 지닐 수 있다고 저자들은 주장한다. 그리고 REM과 Transformer 즉, recurrent modeling, non-recucrrent modeling 이 두 component는 data-driven gated 메커니즘으로 컨트롤될 수 있다.

 

 

Introduction

Sequential Data를 모델링하는데 있어, LSTM, GRU등의 RNN 계열 Recurrent Network 오랜시간동안 benchmark에서 좋은 성능을 보여주었다. 이 성공은 다양한 recurrent dynamics 즉, recurrent inductive bias 덕분이었다. 자세하게는 두 입력 간의 의존성은 상대적인 시간적 위치에 따라 크게 달라지는 parametric form 으로 설명할 수 있다는 것을 의미한다. 그러나 이러한 recurrent model은 우리가 잘 알고 있는 2가지 문제점이 있다. 하나는 gradient vanishing 문제이고 이는 recurrent model은 멀리 떨어져 있는 입력 간의 높은 correlation을 표현하기에는 어렵다는 것을 의미한다. 이 문제는 이전 hidden state가 다음 입력으로 들어가는 recurrent model 구조 상 근본적으로 해결할 수 는 없지만, 긴 메모리 패턴을 도입하는 등의 방법으로 문제를 완화할 수는 있다. 두 번째는, 순차적인 특성으로 인해 병렬적으로 모델을 학습시키기 어렵다는 것이다. recurrent model의 계산 효율성을 개선하기 위해 많은 기법이 제안되었으나 모두 단점을 가지고 있다. 반면 Transformer는 두 토큰 사이의 유사도를 계산해서 long range dependence를 잘 모델링하며 recurrent model과는 다르게 feed-forward가 가능해 병렬 training이 가능하다. 그러나 이러한 transformer의 flexibility는 샘플 비효율성을 낳는다는 단점이 있으며 good generalization ability를 보장하기 위해서는 아주 많은 샘플이 필요하다. 더욱이 트랜스포머에서는 시간 순서가 무시되기 때문에 positional encoding이라는 추가적인 인코딩을 통해 temporal information을 반영해야 한다. 

RNN과 Transformer는 서로 장단점을 가지고 있는데 recurrent model은 recurrent pattern을 작은 샘플이라도 잘 포착하지만 Transformer는 많은 양의 데이터가 있어야 recurrent, non-recurrent 패턴을 포착할 수 있다. 간단하게 말하면 Transformer는 더 많은 데이터가 필요한 대신 global 패턴을 잘 포착할 수 있고 RNN은 적은 데이터로도 recurrent 패턴을 포착할 수 있지만 트랜스포머처럼 global 정보를 포착하기는 힘들다. 이 두 모델을 합치려는 다양한 시도들이 있었지만 긴 입력을 segment로 쪼개서 segment-level recurrence를 도입하는 등의 hierarchical design은 더 정밀한 recurrent dynamics를 간과하게 된다.

 

저자들은 linear activation을 가진 RNN layer는 scalar hidden coefficient를 가진 simple RNN의 시리즈로 쪼개질 수 있다는 점을 발견했다. 각 simple RNN은 distinct recurrent pattern과 simple RNN들의 cobination forms the recurrent dynamics of RNN layer를 유도할 수 있다. 그리고 이는 multihead self attention의 positional encoding과 같음을 보일 수 있다. 이를 사용해서 병렬 연산을 유지하면서, RNN과 self attention을 하나의 연산으로 합치는 솔루션인 Self-Attention with Recurrence(RSA)가 자연스럽게 탄생했다. 

 

Relationship between RNN and Multihead Self-Attention

해당 파트에서는 일반성을 크게 잃지 않고도 Scalar hiden coefficients를 가진 simple RNN series로 RNN layer를 근사화할 수 있고, 이를 Multihead self-attention 형태로 표현될 수 있음을 보인다.

 

Breaking down an RNN layer

RNN layer에서 이전 hidden h_{t-1}와 현재 입력 x_t를 받아 activation function을 통과하여 hiden state를 out한다. 이때 activation function이 linear라고 하고 bias term을 생략하면 (1)의 왼쪽과 같은 식으로 쓸 수 있고 이를 다르게 표현하면 (1)의 오른쪽 식처럼 표현할 수 있다. 이는 feedforward form을 가지고 있음에도 recurrent weight W_h의 power j를 계산해야 하므로 RNN은 병렬로 트레이닝할 수 없다. 이 섹션에서 (1)식의 RNN이 scalar hidden coefficients를 가진 simple RNN 시리즈로 분해될 수 있도록 W_h를 block diagonalize 하는 것을 보인다.

 

R distinct nonzero eigenvalue를 가진 실수 행렬은 모든 d*d 실수 행렬의 셋에서  at most R 랭크를 갖는 dense matrix이다.

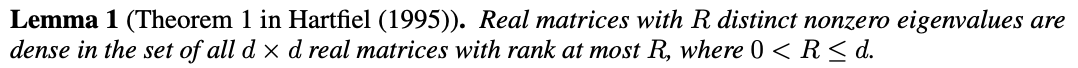
weight matrix W_h가 d보다 작은 R 랭크를 가진다고 가정하면, Lemma 1에 의해, 일반화를 많이 잃지 않고 우리는 W_h의 nonzero eigenvalues는 모두 distinct하다고 가정할 수 있다. 특히 W_h는 r real nonzero eigen value \lambda_1, .. lambda_r을 가지고, s pair의 nonzero 복소수 eigenvalue \lambda_r+1, \lambda_r+2s를 가진다. 그 결과 우리는 W_h를 real Jordan form으로 바꿀 수 있다. W_h=BJB^-1 여기서 B는 d*d invertible 행렬이고 J는 d*d block diagonal matrix이다. 그리고 이는 j가 1보다 큰 모든 j에 대해 만족하며 우리는 W_h에 의해 유도된 recurrence를 p*p block matrices in J(p=1 or 2)로 분해할 수 있다.

 

(1) 식과 비슷하게 우리는 linear activation을 가지는 RNN을 3가지 타입으로 정의할 수 있고 이는 아래 식(2)와 같다.

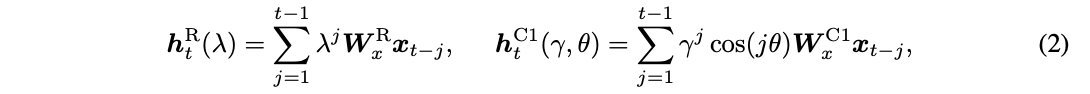
3개의 RNN은 각각 recurrent weight를 \lambda, (\gamma, \theta), 그리고 nonlinear activation function이 주어졌을 때의 형태(Appendix)로 나타냈을 때를 의미한다. 

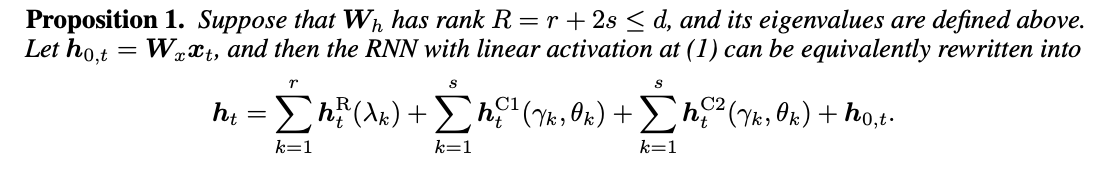
따라서 rank R이 d보다 작은 W_h는 RNN이 linear activation을 가질 때 식(1)을 위 수식처럼 다시 쓸 수 있게 된다.

 

An Equivalent MHSA Representation

d_in의 차원을 가진 T개의 토큰을 포함하는 input matrix X와 h_t^R의 RNN, matrix A의 transpose matrix A'이 있을 때, 선형변환으로 X를 project한 value matrix V(=XW_V)를 먼저 계산하면 relative positional encoding matrix는 식 (3)처럼 표현할 수 있다. 그 결과로 식 (2)의 RNN 중 recurrent weight가 \lambda인 경우 h_t^R(\gamma)를 Self attention 형태로 표현할 수 있게 된다.

그리고 recurrent weight가 (\gamma, \theta)일 때 h_t^Ci는 위 형태로 표현할 수 있게 된다. 그리고 그 중 남은 텀 h_0,t는 오직 x_t에만 의존하므로 inter-depencence가 없다. 수학적으로 이를 identity realitive positonal encoding matrix를 사용해 Self Attention 형태로 나타낼 수 있게 된다. 마지막으로 위 reformulation에서 모든 쿼리, 키 행렬 Q와 K는 0으로 설정된다.

그리고 Proposition 1의 condition을 만족하면, linear activation을 가진 RNN은 키와 쿼리가 0 행렬일 때, head가 r+2s+1개인 multihead self attention으로 표현될 수 있고 relative positional encoding matrices는 각각 P^R_mask(\lambda_k), {P^C1_mask(\gamma_k, \theta_k, P_mask^C2(\gamma_k, \theta_k)}, identity matrix가 된다.

 

(2)식의 3가지 simple RNN은 서로 다른 temporal decay patterns를 제공한다. h_t^R은 real eigenbalue \gamma_k로부터 유도된 regular exponential decaly를 제공하고, {h_t^C1, h_t^C2}는 complex eigenvalue로부터 유도된 cyclical dampled cosine or sine decay를 제공한다. 이러한 temporal decay 패턴들은 regular REM, cyclical REM으로 나타내어질 수 있다. proposition 2에 의해, 이 3가지 타입의 패턴들의 cobination은 (1) 식의 RNN layer의 recurrent dynamics를 형성할 수 있다.

 

 

Encoding Recurrence Into Self-Attention

Proposition 2에서 쿼리와 키 행렬이 MHSA 표현에서 0으로 설정되어 있지만, standard 트랜스포머에서는 중심적인 역할을 한다. 이것이 바로 RNN과 트랜스포머의 강점을 원활하게 결합하기 위해 Self-Attention with Recurrence(RSA) 모듈을 제안하게 된 동기이다.

P는 regular or cyclical REM이고, 각 헤드에서 \sigma(\mu)에서 sigma는 sigmoid function이며 게이트가 되고 mu는 learnable gate-contral parameter이다. 그리고 이전 섹션에서 설명한 REM은 lower triangular matrices이고, 이는 unidirectional RNN을 따른다. non-causal sequential tasks에서, bidirectional RNN가 보통 적용되고, 이에 따라 우리는 REM의 unmasked version을 정의할 수 있다. 

그러면 regular REM, cyclical REM 각각 위처럼 unmasked version을 정의할 수 있게 되는데, 실제로 트랜스포머로부터 나오는 이 두 파라미터 gamma, lambda의 크기는 1을 넘게 된다. 이 문제를 피하기 위해 이 두 파라미터 lambda, gamma를 각각 tahn, sigmoid에 통과시켜 바운드를 한다. 

 

Sequential data는 대게 recurrent pattern을 가지고 있고 이는 REM으로 포착할 수 있게 된다. 반면 그 외 non-recurrent pattern은 일반 트랜스포머의 softmax(QK')을 통해 모델링할 수 있다. REM은 positional encoding과 상호보완적이고, 이는 relative location information도 제공할 수 있다. multiheadd RSA에서는 gate-control parameter mu는 오직 레이어에 따라 달라지는 반면 행렬 P를 제어하는 파라니터는 모든 헤드와 레이어에 따라서 달라진다.