SW 개발
알고리즘 공부

🍄 알고리즘
시간복잡도 및 요약
| 카테고리 | 이름 | 시간복잡도 | 설명 |
| 자료구조 | 유니온 파인드 | O(α(N)) | 서로소 집합 자료구조, 경로 압축 + union by rank |
| 자료구조 | 우선순위 큐 (힙) | 삽입/삭제: O(log N), 조회: O(1) | 최대/최소값을 빠르게 관리하는 큐 |
| 자료구조 | 링크드 리스트 | 삽입/삭제: O(1), 탐색: O(n) | 노드 포인터 기반 구조, 삽입·삭제 효율적 |
| 자료구조 | Trie | 삽입/탐색: O(L) | 문자열 저장 트리, 접두사 탐색에 최적 |
| 완전탐색 | DFS | O(V + E) | 깊이 우선 탐색, 스택/재귀 기반 |
| 완전탐색 | BFS | O(V + E) | 너비 우선 탐색, 큐 기반 |
| 백트래킹 | 백트래킹 | O(조건에 따라 다양) | 상태 공간 트리 탐색, 가지치기 통해 효율화 |
| 탐색 | 이진 탐색 | O(log N) | 정렬된 배열에서 중간 기준 이분 탐색 |
| 최단경로 | 다익스트라 | O((V + E) log V) | 음수 간선 불가, 우선순위 큐 사용 |
| 최단경로 | 플로이드-워셜 | O(V³) | 모든 정점 쌍 간의 최단경로 계산 |
| DP | 동적 계획법 | 문제마다 다름 | 부분 문제를 저장하며 중복 계산 방지 |
| MST | 크루스칼 | O(E log E) | 간선 중심, 정렬 후 유니온파인드 사용 |
| MST | 프림 | O(E log V) | 정점 중심, 우선순위 큐 사용 |
| 위상정렬 | 위상정렬 | O(V + E) | DAG에서 순서 결정, 진입 차수 사용 |
| 그래프 | LCA | O(log N) | 트리에서 두 노드의 최소 공통 조상 찾기 |
| 그래프 | 펜윅 트리 (BIT) | 업데이트/쿼리: O(log N) | 누적합, 구간합 처리에 효율적 |
| 그래프 | 오일러 경로 | O(V + E) | 모든 간선을 정확히 한 번 방문 |
| 기타 | 투 포인터 | O(N) ~ O(N²) | 두 포인터를 움직이며 조건 만족 탐색 |
| 기타 | 구간합 (Prefix Sum) | 쿼리: O(1), 사전 계산: O(N) | 구간합 빠르게 계산, 누적합 배열 사용 |
| 기타 | 세그먼트 트리 | 쿼리/업데이트: O(log N) | 동적 구간합 처리 |
| 기타 | 비트마스킹 | 연산: O(1), 조합: O(2ⁿ) | 상태/집합 표현 및 조합에 활용 |
자료구조
서로소 집합(Disjoint Sets)
- 공통 원소가 없는 두 집합
- {1,2}와 {3,4}는 서로소지만 {2,3}은 아님
1. UnionFind
- Disjoint Set(서로소) 서로 중복되지 않는 부분 집합, 즉 서로소 집합 자료 구조를 표현할 때 사용된다.
- 서로소 집합 자료구조는 합치기 찾기(Union Find) 자료구조라고 불리기도 한다.
- 크루스칼에서 cycle check시도 사용
- 합집합(Union): 두 개의 원소가 포함된 집합을 하나의 집합으로 합치는 연산
- 찾기(Find): 특정한 원소가 속한 집합이 어떤 집합인지 알려주는 연산
- 동작과정
- 합집합(Union) 연산을 확인하여 서로 연결된 두 노드 A, B를 확인한다.
- A와 B의 루트노드 A'과 B'을 찾는다
- 모든 합집합(Union) 연산을 처리할 때까지 1을 반복한다.
- 합집합(Union) 연산을 확인하여 서로 연결된 두 노드 A, B를 확인한다.
- 서로소 집합 자료구조에서는 연결성을 통해 손쉽게 집합의 형태를 확인할 수 있다.
- 루트 노드의 갯수가 집합의 갯수
# Find 루트 노드를 찾을 때까지 재귀 호출
def find_parent(parent, x):
if parent[x] != x:
return find_parent(parent, parent[x])
return x
# Union 두 원소가 속한 집합 합치기
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
# 별다른 조건이 없으면 더 큰 값을 부모로함
if a < b:
parent[b] = a
else:
parent[a] = b
# node 갯수, edge 갯수
v, e = map(int, input().split())
# 부모 테이블 노드 갯수만큼 자기 자신으로 초기화
parent = [i in range(v + 1)]
# Union
for i in range(e):
a, b = map(int, input().split())
union_parent(parent, a, b)
print('각 원소가 속한 집합: ', end='')
for i in range(1, v+1):
print(find_parent(parent, i), end=' ')
print()
print('부모 테이블: ', end='')
for i in range(1, v+1):
print(parent[i], end=' ')
문제점
- 합집합 연산이 편향되게 이루어지는 경우 Find가 비효율적으로 동작한다. 부모 노드를 찾을 때 거슬러 올라가야 하기 때문
- 최악의 경우 Find가 모든 노드를 확인해야 해서 O(V)
- 경로 압축(Path Compression) 이용해 Find 최적화
- Find를 재귀적으로 호출한 후 부모 테이블 값을 바로 갱신
def find_parent(parent, x):
if parent[x] != x:
parent[x] = find_parent(parent, parent[x])
return parent[x]
서로소 집합을 이용한 사이클 판별
- 무방향 그래프의 경우 사이클 판별할 때 사용할 수 있다.
- 참고로 방향 그래프는 DFS를 통해 판별할 수 있음
- 각 간선을 하나씩 확인하며 두 노드의 루트 노드를 확인
- 루트 노드가 서로 다르다면 Union
- 루트 노드가 서로 같으면 Cycle 발생한 것
- 모든 간선에 대하여 1 반복
# find_parent(), union_parent()는 같고,
# Union
cycle = False
for i in range(e):
a, b = map(int, input().split())
if find_parent(parent, a) == find_parent(parent, b):
cycle = True
break
else:
union_parent(parent, a, b)2. 우선순위 큐
- 최단 경로 → 다익스트라 O(V^2) - 노드 5000개 이하일 때, 이상일 때 우선순위 큐 사용
- 우선순위 큐는, 우선순위가 가장 높은 데이터를 먼저 삭제하는 자료구조,
- 스택은 가장 나중에 삽입된걸 삭제하고 큐는 가장 먼제 삽입된 데이터를 삭제하는 자료구조
- 리스트로 구현하면 삽입 O(1), 삭제 O(N)
- 힙으로 구현하면 삽입 O(logN), 삭제 O(logN)
- 단순히 N개의 데이터를 힙에 넣었다가 모두 꺼내는 작업은 정렬과 동일함 (heap정렬 O(logN))
- 힙은 완전 이진 트리 자료구조의 일종
- python은 기본적으로 minheap이고 maxheap구현하고 싶으면 - 붙이면됨
import heapq
def heapsort(iterable):
h, result = [], []
for value in iterable:
heapq.heappush(h, value)
for i in range(len(h)):
result.append(heapq.heappop(h))
return result
n = int(input())
arr = []
for i in range(n):
arr.append(int(input()))
res = heapsort(arr)
for i in range(n):
print(res[i])3. 링크드리스트
- 삽입 삭제가 잦을 때.
- List: find O(N), insert O(N), Delete O(N)
- Linkedlist : find O(N), insert O(1), Delete O(1)
- 위로만, 아래로만 뺴는 경우 싱글, 위 아래 둘다 넣고 뺴야하는 경우 더블링크드리스트
- 더블 링크드리스트 예제 : 코드트리 > 산타의선물공장
4. Trie
- 집합(set)에서 특정 키를 찾는데 사용되는 m-ary 자료구조 중 하나이다.
- m-ary는 최대로 가질 수 있는 자식 수를 말하고 m=2이면 이진트리이다.
- 문자열 조회를 빠르게 하기 위해 사용되므로 자동완성 등에 많이 사용된다.
- 꼭 문자열에만 사용되는 것은 아니고 비트와 같이 순서가 있는 열거 가능한 자료형에도 사용할 수 있다.
- n개의 단어 사전에서 길이 m의 단어를 일일히 비교해가며 찾으면 이진 검색 트리를 사용해도 O(mlogn)이 필요하다.
- 겹치는 문자열이 없는 경우 O(포인터크기 * 포인터갯수 * 총노드수)의 메모리가 필요하다
- 비트를 통해 최적화 하는 방법이 있다
문제 백준 전화번호 목록
# 트라이 자료구조
import sys
input = sys.stdin.readline
class Node(object):
def __init__(self, has_end=False):
self.has_end = has_end
self.children = dict()
class Trie(object):
def __init__(self):
self.head = Node(None)
# 트라이에 전화번호 추가
def insert(self, num):
curr_node = self.head
for d in num:
# 현재 노드에 해당하는 숫자의 자식이 없으면 생성
if curr_node.children.get(d) is None:
curr_node.children[d] = Node()
# 해당하는 숫자 자식으로 이동
curr_node = curr_node.children[d]
# 자료구조 말단에서 끝 표시
curr_node.has_end = True
# 트라이에서 전화번호 조회
def search(self, num):
curr_node = self.head
for d in num:
# 해당하는 숫자의 자식이 없으면 전화 가능하므로 일관성 있음
if curr_node.children.get(d) is None:
return True
curr_node = curr_node.children[d]
# 현재 위치에서 끝나는 전화번호가 있다면 해당 번호로 전화되므로 일관성 없음
if curr_node.has_end:
return False
return True
if __name__=="__main__":
t = int(input())
for _ in range(t):
n = int(input())
phone_numbers = [input().rstrip() for _ in range(n)]
# 길이가 짧은 것 부터 삽입하기 위해 정렬
phone_numbers = list(map(lambda x : (len(x), x), phone_numbers))
phone_numbers.sort(key = lambda x : x[0])
data = Trie()
# 번호에 대해 일관성 있는지 확인후 Trie 자료구조 데이터에 삽입
for _, number in phone_numbers:
# 일관성 없으면 즉시 NO 출력후 다음 테스트케이스 탐색
if data.search(number) == False:
print("NO")
break
# 일관성 있으면 데이터 삽입
data.insert(number)
# 모든 전화번호가 일관성 있다면 YES 출력
else:
print("YES")
탐색
- 경우의 수 나눠서 그래프 그려보기
1. 완전 탐색
- 가능한 모든 방법을 찾아봐서 해를 구하는 것
- 그래프 탐색 : DFS, BFS
- BFS : 큐에서 노드 꺼내고 해당 노드의 인접 노드 중 방문하지 않은 노드를 모두 큐에 삽입하고 방문처리
- DFS : 보통 재귀로. 함수 시작 부분에 종료 조건 명시. 익숙하지 않을 때 방문 경로 저장같은 거 global로 하면 안헷갈림
방향그래프의 사이클 판별 (DFS)
- 무방향 그래프의 경우 UnionFind를 통해 사이클을 판별할 수 있고
- 방향 그래프의 경우 DFS를 통해 판별할 수 있다.
- DFS로 순회하면서 다음 방문할 곳이 이미 방문했고 재귀를 시작한 곳이라면 cycle을 이룬 것.
백준 10451번 순열 사이클
from sys import stdin
input = stdin.readline
# 재귀로 현 숫자가 가리키는 다음 숫자 확인
def dfs(startNum, originNum):
global cycle
nextNum = A[startNum] # 현 숫자가 가리키는 다음 숫자
if check[nextNum]: # 이미 방문했다면 사이클 이루는지 확인
if nextNum == originNum:
cycle += 1 # 사이클 이룬 것이므로 +1
return
else: # 첫 방문이라면 방문 표시
check[nextNum] = 1
dfs(nextNum, originNum) # 재귀로 다음 숫자 확인
# main
T = int(input())
for _ in range(T):
N = int(input())
A = [0] + list(map(int, input().split()))
cycle = 0
check = [0] * (N+1) # 방문 표시
for start in range(1, N+1):
if check[start]: # 이미 방문한 곳이면 탐색 X
continue
check[start] = 1 # 새로 탐색 시작
dfs(start, start) # 이동할 숫자와 사이클 확인용 시작한 숫자
print(cycle)DFS로 연결 요소 찾기 (Connected Component)
n, m = 4, 5
graph = [[0,0,1,1,0], [0,0,0,1,1], [1,1,1,1,1], [0,0,0,0,0]]
result = 0
def dfs(x, y):
if x > 0 and x < n and y > 0 and y < m:
if graph[x][y] == 0:
graph[x][y] == 1
dfs(x+1, y)
dfs(x-1, y)
dfs(x, y+1)
dfs(x, y-1)
return True
return False
for i in range(n):
for j in range(m):
if dfs(n, m) == True:
result += 1BFS로 최단경로 찾기
- BFS : queue 이용, 큐에서 노드 꺼내고 해당 노드의 인접 노드 중 방문하지 않은 노드를 모두 큐에 삽입하고 방문처리
- BFS는 간선의 비용을 이용해 최단거리를 찾는 문제에도 이용
n, m = 5, 6
_map = [[1,0,1,0,1,0],
[1,1,1,1,1,1],
[0,0,0,0,0,1],
[1,1,1,1,1,1],
[1,1,1,1,1,1]]
dx = [-1,1,0,0]
dy = [0,0,-1,1]
print(bfs(x,y))
def bfs(x,y):
queue = deque()
queue.append(x,y)
while queue:
x, y = queue.popleft()
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
if nx < 0 or nx >=n or ny < 0 or ny >= m:
continue
if graph[nx][ny] == 0:
continue
if graph[nx][ny] == 1:
graph[nx][ny] == graph[x][y] + 1
queue.append((nx,ny))
return graph[n-1][m-1]2. 백트래킹

- DFS와의 차이
- 예시 : 그래프나 트리의 모든 노드를 탐색, 경로 찾기(미로 찾기), 그래프 연결성 확인, 경로 존재 여부 탐색
- 탐색 목표 : 모든 노드 방문
- 한 경로를 끝까지 탐색한 후 다른 경로로 넘어감.
- 예시 : 특정조건(제약조건)을 만족하는 해를 찾는 문제, 퍼즐, N-queen(퀸이 서로 공격하지 않는 배치를 찾는 문제), 순열과 조합
- 탐색 목표 : 최적의 해를 찾을 때, 조건을 만족하는 해를 찾을 때
- 모든 가능한 해를 시도하면서도 조건을 만족하지 않는 경로는 미리 Pruning하여 효율성을 높이므로 DFS보다 시간을 줄일 수 있다.
- 비트마스킹, DP 등을 활용해 Pruning하여 시간 최적화.
- 상태공간트리 를 그려보고 새로운 탐색이 무의미하다고 생각되면 자르기.
- 상태공간트리에서 depth를 내려갈 때마다 조건 체크.
백트래킹 문제들
| 백준 N-Queen | Gold 4 | 백트래킹 Well-known 문제 |
| 백준 소문난 칠공주 | Gold 3 | BFS와 같지만 Y가 4개 이상인 루트는 탐색하지 않음(백트래킹), 십자모양탐색(DFS로 조합찾고 BFS로 인접체크) |
| 백준 Don’t Get Rooked | Gold 5 | |
| SWEA 4317 칩생산 | Gold 5 | 1x1사이즈 방문이 아니고 2x2사이즈 모두 방문가능해야 방문 > DFS인데 현재칸 방문 + 다음칸 방문 동시에, 한 열 or 행 쭉 따라서 방문하고 도달하면 행 or 열 바꾸기 / 비트마스킹, DP로 탐색 최적화 |
| 백준 낚시왕 | Gold 1 | 배열 늘려서 탐색하는 문제 |
3. 이진 탐색
- 탐색 범위를 반씩 좁혀가며 데이터를 탐색
- 리스트가 정렬되어 있을 때
- 탐색 범위가 큰 경우
- 특정 원소를 찾기 위해 앞에서부터 그냥 확인하는 것 → 순차 탐색
- 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법으로 리스트가 정렬되어 있을 때 씀 O(logN) → 탐색 범위가 큰 경우 떠올려야 함
def binary_search(arr, target, start, end):
if start > end:
return None # 찾을 수 없는 경우
mid = (start + end) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
return binary_searcy(arr, target, mid + 1, end)
else:
return binary_search(arr, target, start, mid - 1)
# mid + 1, mid - 1을 해주어야 while s <= e 에서 무한루프 걸리지 않음정렬된 배열에서 특정 수의 갯수 구하기 (bisect) 이용
- N개의 원소를 포함하고 있는 수열이 오름차순으로 정렬되 있습니다. 이때 수열에서 x가 등장하는 횟수를 계산하시오.
- 예를 들어수열 {1, 1, 2, 2, 2, 2, 3}이 있고 x=2이면, 현재 수열에서 값이 2인 원소가 4개 이므로 4를 출력합니다.
- 이 문제는 시간복잡도 O(logN)으로 설계하지 않으면 시간 초과 판정을 받는 문제
from bisect import bisect_left, bisect_right
def count_by_range(arr, left_val, right_val):
right_index = bisect_right(arr, right_val)
left_index = bisect_left(arr, left_val)
return right_index - left_index
- 특정 값이 등장하는 첫번째 위치 bisect_left와 마지막 위치 bisect_right를 찾아 위치 차이를 계산해서 문제를 해결
최단경로
- 모든 노드를 연결하는 경로 중 비용이 최소가 되는 경로
1. 다익스트라 (Dijkstra) - Greedy
- 매 상황에서 가장 비용이 적은 노드를 선택해 임의의 과정을 반복하므로 Greedy로 분류하지만 DP의 원리가 적용된 것임.
- 특정 노드에서 출발해 다른 모든 노드로 가는 최단 경로를 계산
- 한 지점에서 다른 특정 지점까지 최단경로 → 1차원 리스트에 저장
- algorithm
- 출발 노드 설정
- 최단 거리 테이블 초기화
- 방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 선택
- 이렇게 선택된 최단 거리가 가장 짧은 노드는 바뀌지 않기 때문에 그리디
- 해당 노드를 거쳐 다른 노드로 가는 비용을 계산해 최단 거리 테이블 갱신
- 3, 4 반복
- 이렇게 하면 최단 거리를 알 수 있는데, 경로를 출력하려면 추가적인 작업 필요
다익스트라 O(V^2)
import math
n, m = 6, 7
# graph[i] = [(j, c), ..]
# node i에서 node j로 가는 비용이 c
graph = [[], [(2, 2), (4, 1)], [(1, 2), (4, 2), (3, 3)],
[(2, 3), (6, 5)], [(1, 1), (2, 2), (5, 1)],
[(4, 1), (6, 2)], [(5, 2), (3, 5)]]
distance = [math.inf] * (n + 1)
visited = [False] * (n + 1)
def get_min_node():
index = -1
min_val = math.inf
for i in range(1, n + 1):
if not visited[i] and min_val > distance[i]:
min_val = distance[i]
index = i
return index
def dijkstra(start):
distance[start] = 0
visited[start] = True
for j, c in graph[start]:
distance[j] = c
for _ in range(n - 1): # while all(visited)와 같음, 모든 노드 방문 위해
cur = get_min_node()
visited[cur] = True
# cur을 거쳐 이동하는 경우가 더 짧은 경우
for j, c in graph[cur]:
cost = distance[cur] + c
if distance[j] > cost:
distance[j] = cost
dijkstra(1)
for i in range(1, n + 1):
if distance[i] == math.inf:
print('INF')
else:
print(distance[i])다익스트라 우선순위 큐(삽입, 삭제 O(NlogN) 사용)
import heapq
import math
n, m = 6, 7
# graph[i] = [(j, c), ..]
# node i에서 node j로 가는 비용이 c
graph = [[], [(2, 2), (4, 1)], [(1, 2), (4, 2), (3, 3)],
[(2, 3), (6, 5)], [(1, 1), (2, 2), (5, 1)],
[(4, 1), (6, 2)], [(5, 2), (3, 5)]]
distance = [math.inf] * (n + 1)
def dijkstra(start):
q = []
heapq.heappush(q, (0, start))
distance[start] = 0
while q:
dist, cur = heapq.heappop(q)
if distance[cur] > dist: # visitied check와 같은 역할, 이미 처리된 노드 무시
continue
for j, c in graph[cur]:
cost = dist + c
if cost < distance[j]:
distance[j] = cost
heapq.heappush(q, (cost, j))
dijkstra(1)
for i in range(1, n + 1):
if distance[i] == math.inf:
print('INF')
else:
print(distance[i])
- 노드 5000개 이하일 때 사용 이상일 때 우선순위 큐(삽입, 삭제 O(NlogN)) 사용
- 기본 원리는 동일하고, 각 단계마다 방문하지 않는 노드 중 최단 거리가 가장 짧은 노드를 선택(get_min_node())할 때 힙(Heap) 자료구조를 이용하는 것만 다름.
- 힙구조 사용 다익스트라 → O(ElogV)
- while은 최대 노드 갯수 V임.
- 인접 노드 확인하는 총횟수는 최대 E
- E개의 원소를 우선순위 큐에 넣었다가 모두 빼는 연산과 유사하며 O(ElogE)이고 중복 간선을 포함하지 않으면 O(ElogV)가 되는 것
- 음의 가중치를 허용하지 않음
2. 플로이드워셜 (Floyd-Warshall) - DP
- DP, O(N^3) 이므로 노드의 개수가 적은 경우에 사용, 그렇지 않으면 다익스트라
- 즉, 노드가 500개 이하, 모든 노드 - 모든 노드 간 최단거리 구할 때 사용
- 모든 지점에서 다른 모든 지점까지 최단경로 → 2차원 리스트에 저장
- 다익스트라와 마찬가지로 단계별로 거쳐 가는 노드를 기준으로 알고리즘을 수행
- 다익스트라와 다르게 매 단계마다 방문하지 않은 노드 중 최단 거리를 갖는 노드를 찾는 과정이 필요하지 않다.
- 점화식 $D_{ab} = \min (D_{ab}, D_{ak} + D_{kb}$
- 각 단계마다 특정 노드 k를 거쳐 가는 경우를 확인하는데,
- a에서 b로 가는 최단 보다 a에서 k를 거쳐 b로 가는 거리가 더 짧은지 검사
import math
n, m = 6, 7
# graph[i] = [(j, c), ..]
# node i에서 node j로 가는 비용이 c
tmp = [[], [(2, 2), (4, 1)], [(1, 2), (4, 2), (3, 3)],
[(2, 3), (6, 5)], [(1, 1), (2, 2), (5, 1)],
[(4, 1), (6, 2)], [(5, 2), (3, 5)]]
graph = [[math.inf] * (n+1) for _ in range(n+1)]
for i in range(1, n+1):
graph[i][i] = 0
for j, c in tmp[i]:
graph[i][j] = c
# for 문 순서주의 : K (경유지) -> 시작지 I -> 도착지 J
for k in range(1, n+1):
for i in range(1, n+1):
for j in range(1, n+1):
graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])
# result
for a in range(1, n+1):
for b in range(1, n+1):
if graph[a][b] == math.inf:
print('INF', end=' ')
else:
print(graph[a][b], end=' ')
print()⭐️ For 문 순서 왜 K (경유지) -> 시작지 I -> 도착지 J 냐면,
경유점 k를 순차적으로 먼저 접근해야 DP의 전제인
i-j-k의 최단 거리는 i-k 최단거리 + k-j 최단거리 이다가 성립
노드가 1,2,3 있는 경우
자기 자신으로 가는 경로를 제외하고 1>2, 1>3, 2>1, 2>3, 3>1, 3>2를 찾아야 한다
K 고정시 순서가
k=1 1>1>2, 1>1>3, 2>1>1, 2>1>3, 3>1>1, 3>1>2
k=2 1>2>2, 1>2>3, 2>2>1, 2>2>3, 3>2>1, 3>2>2
k=3 1>3>2, 1>3>3, 2>3>1, 2>3>3, 3>3>1, 3>3>2
k=3 1>3>2 일때 1 > 2로 가능한 모든 경로 갱신 후이고, 마지막 경로가 되서 최단 경로를 찾을 수 있다.
i - k - j 인 경우
i=1 1>1>1 1>1>2 1>1>3 1>2>1 1>2>2 1>2>3 1>3>1 1>3>2 1>3>3
i=2 2>1>1 2>1>2 2>1>3 2>2>1 2>2>2 2>2>3 2>3>1 2>3>2 2>3>3
i=3 3>1>1 3>1>2 3>1>3 3>2>1 3>2>2 3>2>3 3>3>1 3>3>2 3>3>3
i=1에서 1>1>3 1>2>3 1>3>3 에서 1>3 경로 거리를 업데이트 해버림
하지만 이때 2>3과 3>3은 아직 갱신이 안된 상태라 최단 경로가 아님
경유지 노드를 고려하기 전에 특정 노드 쌍에 대한 최단 경로를 먼저 고려해버림
동적 계획법(DP, Dynamic Programming)
- 그리디, 구현, 완전탐색 고려 후 풀이 방법이 떠오르지 않거나 시간이 오래걸릴 것 같으면 DP를 고려.
- 점화식을 떠올릴 수 있어야 한다.
- DP가 코테에 나오면 어렵다.
- Dynamic은 자료구조의 동적할당 같은 의미랑 상관없음. 별 뜻 없음
- DP의 사용 조건
- 최적 부분 구조(Optimal Substructure) : 큰 문제를 작은 문제로 나눌 수 있다.
- 중복되는 부분 문제(Overlapping Subproblem) : 동일한 작은 문제를 반복적으로 해결.
- DP solution
- Top -> Down (하향식, 메모이제이션, 재귀 사용)
- Down -> Top (DP의 전형적인 형태)
- DP와 분할 정복은 최적 부분 구조를 가질때 사용한다는 점은 같지만
- DP는 각 부분 문제들이 서로 영향을 미치며 부분 문제가 중복 되지만,
- 분할 정복은 동일한 부분 문제가 반복적으로 계산되지 않는다.
- ex) 퀵정렬. 한 번 Pivot이 자리를 변경해서 자리 잡으면 그 pivot의 위치는 바뀌지 않고, 분할 이후 해당 Pivot을 다시 처리하는 부분 문제는 호출하지 않는다.
- 그리디, 구현, 완전탐색 아이디어로 해결할 수 있는지 검토하고 풀이 방법이 떠오르지 않거나 완전탐색 같은 것이 시간이 오래 걸릴 것 같으면 DP를 고려해 볼것.
- 일단 재귀 함수로 비효율적인 완전 탐색 프로그램을 작성하고 (탑다운) 작은 문제에서 구한 답이 큰 문제에서 그대로 사용될 수 있으면, 메모이제이션으로 코드를 개선하는 방법으로 DP를 사용할 수 있다.
- EX) 소프티어 염기서열 : 완전탐색으로 풀렸지만 시간초과났음.
- EX) 프로그래머스 N으로 표현 : DFS로 풀면 속도가 100배 차이남
- DP가 코테에 나올 경우 기본 유형 문제가 나올 확률이 높은데, DP의 점화식을 떠올리는데 시간이 많이 소요되기 때문.
DP Well-known 문제 - 외판원 순회(TSP, Travelling Salesman Problem)
- https://www.acmicpc.net/problem/2098 : 비트마스킹 해야함
- https://www.acmicpc.net/problem/10971 : DFS + memoriaztion으로도 가능
# 비트마스킹 없이
N = int(input())
W = [list(map(int, input().split())) for _ in range(N)]
# W[i][j] > i에서 j로 가기 위한 비용, asymmetric, W[i][j] =/= W[j][i]
INF = float('inf')
def dfs(cur, route):
if tuple(route) in dp[cur]:
return dp[cur][tuple(route)]
if len(route) == N:
return W[cur][0] if W[cur][0] > 0 else INF
min_d = INF
for nxt in range(N):
if nxt not in route and W[cur][nxt] > 0:
d = W[cur][nxt] + dfs(nxt, sorted(route + [nxt]))
min_d = min(min_d, d)
dp[cur][tuple(route)] = min_d
return min_d
dp = {i: {} for i in range(N)}
print(dfs(0, [0]))# 비트마스킹
N = int(input())
W = [list(map(int, input().split())) for _ in range(N)]
# W[i][j] > i에서 j로 가기 위한 비용, asymmetric, W[i][j] =/= W[j][i]
INF = float('inf')
def dfs(cur, route):
if dp[cur][route]:
return dp[cur][route]
if route == (1 << (N-1)) - 1:
return W[cur][0] if W[cur][0] > 0 else INF
min_d = INF
for nxt in range(1, N):
if W[cur][nxt] and not route & (1 << (nxt - 1)):
d = W[cur][nxt] + dfs(nxt, route | (1 << (nxt - 1)))
min_d = min(min_d, d)
dp[cur][route] = min_d
return min_d
dp = [[0] * (1 << (N-1)) for _ in range(N)]
print(dfs(0, 0))DP 문제 - 1로 만들기 (https://www.acmicpc.net/problem/1463)
- 1이될때까지 라는 문제는 n이 무엇이든 1로 빼는 것보다 나누는 것이 값을 빠르게 줄일 수 있어 Greedy 였지만, 이 문제는 당장 큰 수로 나누는 것 보다 다른 연산과 섞었을 때 더 빠르게 값을 줄일 수 있는 경우가 존재할 수 있기 때문에 그리디X
- 최적 부분 구조와 중복되는 부분 문제를 만족.
- $a_i = i$를 1로 만들기 위한 최소 연산 횟수
- 점화식 $a_i = \min (a_{i-1}, a_{i/2}, a_{a/3} + 1$
- 1을 빼는 연산을 제외하고는 해당 수로 나누어떨어질 때에 한해 점화식을 적용
# 1 Bottom up
# dp의 index가 n이고 value가 연산 횟수이다.
# index 2는 index 1에서 -1 연산 한번 해서 만들어진 것 이므로 dp[2] = 1
dp = [0] * n
for i in range(2, n+1):
dp[i] = dp[i-1] + 1
if i % 2 == 0:
# 이전 값에서 -1 한 것 누적횟수
# 2로 나눈 값에서 -1 한 것 누적횟수
# 중 더 작은거
dp[i] = min(dp[i], dp[i // 2] + 1)
if i % 3 == 0:
dp[i] = min(dp[i], dp[i // 3] + 1)# 2 Top Down 재귀
# 애가 더 빨랐음
dp={1:0}
def rec(n):
if n in dp.keys():
return dp[n]
if (n%3==0) and (n%2==0):
dp[n]=min(rec(n//3)+1, rec(n//2)+1)
elif n%3==0:
dp[n]=min(rec(n//3)+1, rec(n-1)+1)
elif n%2==0:
dp[n]=min(rec(n//2)+1, rec(n-1)+1)
else:
dp[n]=rec(n-1)+1
return dp[n]# 3. BFS
from collections import deque
x=int(input())
Q=deque([x])
visited=[0]*(x+1)
while Q:
c=Q.popleft()
if c==1:
break
if c%3==0 and visited[c//3]==0:
Q.append(c//3)
visited[c//3]=visited[c]+1
if c%2==0 and visited[c//2]==0:
Q.append(c//2)
visited[c//2]=visited[c]+1
if visited[c-1]==0:
Q.append(c-1)
visited[c-1]=visited[c]+1
print(visited[1])DP 문제 - 배낭문제
# 1차원 DP
N, M = map(int, input().split(' '))
dp = [0 for _ in range(M + 1)]
objects = [tuple(map(int, input().split())) for _ in range(N)]
for W, C in objects:
for i in range(M, W - 1, -1):
dp[i] = max(dp[i], dp[i - W] + C)
print(dp[M])최소 신장 트리(MST, Minimum Spanning Tree)
- 모든 노드를 포함하되 사이클이 없는 최소비용 tree(MST)를 만들기 위한 알고리즘
- MST의 전체 edge 갯수는 node 갯수 - 1이다. E = V - 1
- spanning tree는 cycle이 존재하지 않고, 모든 노드를 포함하는 트리
- node가 n개면 edge는 n-1개
- MST는 모든 노드를 최소 비용으로 연결하는 트리
- 크루스칼과 프림 알고리즘이 있다
1. 크루스칼 (Kruskal) 알고리즘
- 그리디 알고리즘
- 정렬부분 때문에 O(ElogE)
- UnionFind 사용
- 동작과정
- 간선을 비용에 따라 오름차순으로 정렬 (비용이 적은 간선부터 확인하므로 그리디)
- 간선을 하나씩 확인하며 사이클(같은 집합에 속했는지, Find) 체크(union find이용)
- 사이클 X → MST에 포함시킴(Union)
- 사이클 O → MST에 포함X
- 모든 간선에 대해 1-2 반복
v, e = 7, 9
# (cost, start_node, end_node)
graph = [(29, 1, 2), (75, 1, 5), (35, 2,3),
(34, 2, 6), (7, 3, 4), (23, 4, 6),
(13, 4, 7), (53, 5, 6), (25, 6, 7)]
graph.sort()
# 루트노드
def find_parent(parent, v):
if parent[v] != v:
# 원래는 바로 직전 부모를 parent에 저장하는데
# 그냥 가장 최상단 root 노드를 parent로 저장하므로
# 재귀는 2번밖에 안됨
parent[v] = find_parent(parent, parent[v])
return parent[v]
# 부모를 같게 만드는 연산 Union 연산
def union_parent(parent, a, b):
a = find_parent(parent, a)
b = find_parent(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
parent = [i for i in range(v + 1)]
total_cost = 0
for cost, s, e in graph:
# 부모 다름, Cycle X
if find_parent(parent, s) != find_parent(parent, e):
union_parent(parent, s, e)
total_cost += cost
print(total_cost)
2. 프림 (Prim) algorithm
- 크루스칼의 경우 O(eloge)이고, 프림은 O(n^2)이다.
- 프림도 그리디 Priority Queue(heapq) 사용
- 그래프 내에서 적은 숫자 간선을 가지는 희소 그래프 (Sparse graph)인 경우는 크루스칼
- 밀집 그래프 (Dense graph)인 경우는 프림이 적합.
- 동작 과정
- 시작 정점과 연결된 모든 간선을 Priority Queue에 삽입
- 최소 가중치의 간선 선택
- 선택한 간선의 root가 트리에 포함되어 있지 않으면, Union + 인접 간선 모두 PQ에 삽입
- 모든 정점이 트리에 포함될 때까지 3,4 반복
문제
- 백준 1717, 백준 4195
import heapq
graph = {
'A': {'B': 1, 'C': 4},
'B': {'A': 1, 'C': 2, 'D': 5},
'C': {'A': 4, 'B': 2, 'D': 1},
'D': {'B': 5, 'C': 1}
}
def prim(graph, start):
mst = []
visited = set()
edges = [] # priority queue
count, cost = 0, 0
heapq.heappush(edges, (0, start))
# 이동가능한 노드가 없거나 모든 노드 방문(e = v - 1)할 경우 stop
while edges and count < len(graph) - 1:
w, node = heapq.heappop(edges)
if node not in visited:
cost += 1
count += 1
visited.add(node)
mst.append((node, w))
for node, weight in graph[node].items():
heapq.heappush(edges, (weight, node))
if count != len(graph) - 1:
return '고립 노드가 있어 모두 연결 할 수 X'
else:
return f'total weight: {cost}'
print(prim(graph, 'A'))
3. 위상 정렬 (Topology Sort)
- cycle이 없는, 방향 그래프 DAG(Direct Acycle Graph) 여야 한다.
- 사이클이 있다면 각 노드는 모두 InDegree는 1 이상이므로 큐에 넣을게 없어 위상 정렬 할 수 없음
- ex. 선수과목이 있을 때 적절한 학습순서
- 한번 방문한 노드는 다시 Q에 들어가지 않고, 엣지도 다시 보지 않으므로 O(V+E)
방법
- DFS
- 큐 이용
- indegree가 0인 모든 노드를 큐에 넣고
- 큐가 빌때 까지 아래 과정 반복
-
- 큐에서 원소를 꺼내 해당 노드에서 나가는 outdegree 간선을 제거
- 새롭게 진입차수가 0이된 노드를 큐에 삽입
-
- 결과적으로 각 노드가 큐에 들어온 순서가 위상 정렬을 수행한 결과와 같아진다.
from collections import deque
v, e = 7, 8
edges = [(1,2), (1,5), (2,3), (2,6), (5,6), (3,4), (6,4), (4,7)]
graph = [[] for i in range(v+1)]
indegree = [0] + (v + 1)
for s, e in edges:
graph[s].append(e)
indegree[b] += 1
def topology_sort():
result = []
q = deque()
for i in range(1, v+1):
if indegree[i] == 0:
q.append(i)
while q:
cur = q.popleft()
result.append(cur)
for i in graph[cur]:
indegree[i] -= 1
if indgree[i] == 0:
q.append(i)
for i in result:
print(i, end=' ')
topology_sort()
# 1 2 5 3 6 4 7
# 1 5 2 3 6 4 7
# ...
# 여러 답 존재
# 모든 노드를 방문하기 전에 Q가 빈다면 사이클 존재그래프
1. LCA(Lowest Common Ancestor) 최소 공통 조상
- 모든 노드에 대한 깊이(depth)를 계산
- 최소 공통 조상을 찾을 두 노드를 확인
- 먼저 두 노드의 깊이가 동일하도록 거슬러 올라감
- 이후에 부모가 같아질 때까지 반복적으로 두 노드의 부모 방향으로 거슬러 올라감
- 모든 LCA(a,b) 연산에 대해 2번의 과정을 반복
- 매 쿼리 lca(a,b)마다 부모 방향으로 거슬러 올라가기 위해 최악의 경우 O(N)
- 쿼리 갯수 M이면 O(NM)
문제 백준11437
import sys
sys.setrecursionlimit(int(1e5))
n = int(input())
parent = [0] * (n+1)
d = [0] * (n+1) # 깊이 저장
c = [0] * (n+1) # 방문 여부 (깊이 저장 여부)
graph = [[] for _ in range(n+1)]
for _ in range(n-1):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
# dfs로 depth 저장하기
def dfs(x, depth):
c[x] = True
d[x] = depth
for y in graph[x]:
if c[y]:
# 이미 depth를 구한경우
continue
parent[y] = x
dfs(y, depth + 1)
def lca(a, b):
# 먼저 깊이를 맞춰주기
while d[a] != d[b]:
if d[a] > d[b]:
a = parent[a]
else:
b = parent[b]
# 부모가 같을 때까지 거슬러 올라가기
while a != b:
a = parent[a]
b = parent[b]
return a
dfs(1, 0)
m = int(input())
for i in range(m):
a, b = map(int, input().split())
print(lca(a,b))2. 바이너리 인덱스 트리(BIT, Binary Indexed Tree), 펜윅 트리(Fenwick Tree)
- 2진법 인덱스 구조를 사용해 구간 합 문제를 효과적으로 해결할 수 있는 자료구조
- 세그먼트 트리의 변형으로 수열의 구간 합을 빠르게 계산
- 세그먼트 트리와 마찬가지로 O(logN) 시간에 구간 합을 계산할 수 있고 세그먼트 트리에 비해 적은 공간이 필요하고 구현하기 쉽다는 장점이 있음
- -7은 7의 2진수 표기에서 flip을 한 후 +1을 해준 것
- 7의 경우 0이 아닌 가장 마지막 비트는 00..00111에서 가장 마지막인 1이다
- 이를 알기 위해서 7 & -7 를 하면 된다
- 정수 3은 0이 아닌 마지막 비트 1, 정수 4는 4
- 0이 아닌 마지막 비트를 BIT배열에서 저장하고 있는 값들의 갯수로 사용한다.
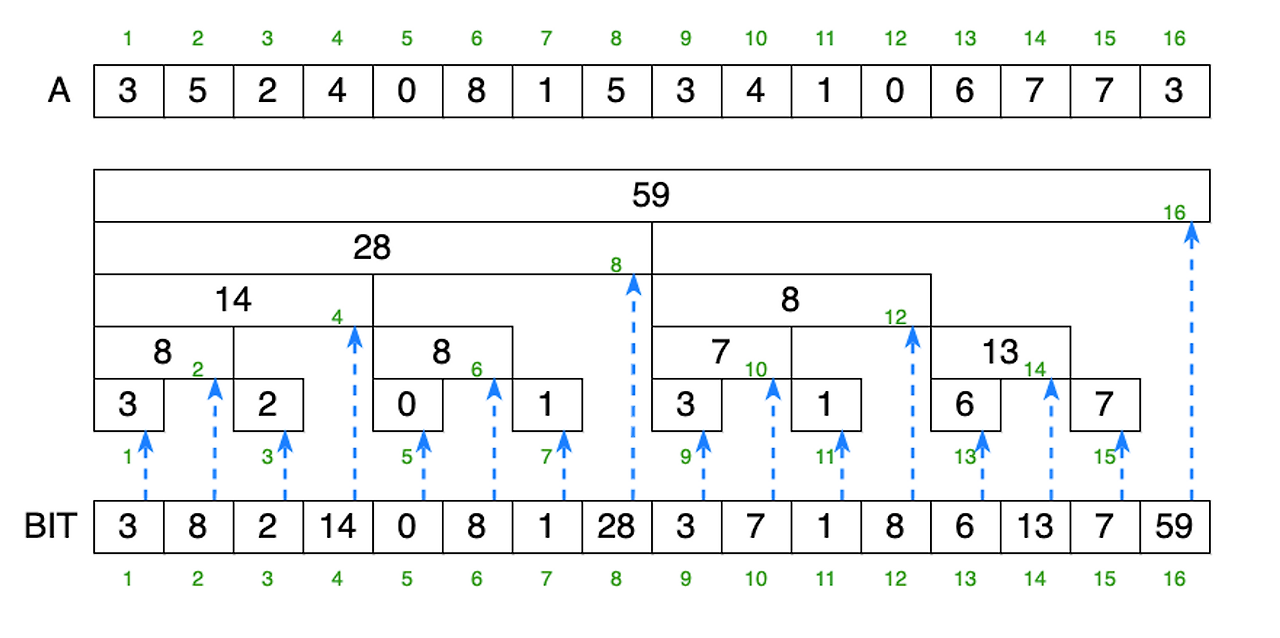
- 사이즈 n짜리 배열에 세그먼트 트리를 만들려먼 2n-1만큼의 배열이 필요하지만, 펜윅 트리는 n만큼의 배열이 필요하다.
- 배열 A에 값이 담겨 있고, BIT에는 저장하고 있는 값들의 갯수이다. 예를 들어 BIT의 인덱스가 i이고 0아닌 마지막 비트가 4라면, A[i-3], A[i-2], A[i-1], A[i]의 합을 가지고 있다.
- BIT에서 index=1은 0아닌 마지막 비트가 1이기 때문에 A배열의 1~1까지 값을 가지고 있고
- BIT에서 index=2은 0아닌 마지막 비트가 2이기 때문에 A배열의 1~2까지 값을 가지고 있고
- BIT에서 index=3은 0아닌 마지막 비트가 1이기 때문에 A배열의 3~3까지 값을 가지고 있고
- BIT에서 index=12은 0아닌 마지막 비트가 4이기 때문에 A배열의 9~12까지 값을 가지고 있고
- BIT에서 index=16은 0아닌 마지막 비트가 16이기 때문에 A배열의 1~16까지 값을 가지고 있고
예시 문제
- 백준 '구간 합 구하기'
- 어떤 N개의 수가 주어져 있고 중간 수에 변경이 빈번히 일어나고 그 중간에 어떤 부분 합을 구하려 한다. 만약 1,2,3,4,5가 있을 때 3번째 수를 6으로 바꾸고 2~5의 합을 구하라고 하면 답은 17이다.
- 이와 같은 문제는 변경이 빈번하므로 값 변경 O(N), 구간 합 계산 O(K)로 O(NK)이므로 비효율적이다.
- 펜윅을 사용하면, 값 변경이 O(logN)이다. 예를 들어 A[3]의 값을 바꿨다면, A[3] 값이 포함된 BIT[3], BIT[4], BIT[8], BIT[16]의 값만 변경해 update하면 된다.
- 구간 합(Prefix Sum)을 구할 때 0이 아닌 마지막 비트만큼 빼면서 구간 합을 계산 O(logN)
- 11에서 시작해서, 11의 0아닌비트는 1이므로 -1칸 이동해 BIT[10]을 더하고
- 10에서 0아닌비트는 2이므로 -2칸 이동해 BIT[8]을 더한다.
- 최종 O(logN) * O(logN) = O(logN)
n, m, k = map(int, input().split())
arr = [0] * (n+1)
tree = [0] * (n+1)
def prefix_sum():
result = 0
while i > 0:
result += tree[i]
i -= (i & -i)
def update(i, dif):
while i <= n:
tree[i] += dif
i += (i & -i)
def interval_sum(start, end):
return prefix_sum(end) - prefix_sum(start - 1)
for i in range(1, n+1):
x = int(input())
arr[i] = x
update(i, x)
for i in range(m + k):
a, b, c = map(int, input().split())
if a == 1: # update
update(b, c - arr[b]) # dif = 바뀐 크기
arr[b] = c
else: # 구간 합 연산
print(interval_sum(b, c))3. 오일러 경로(Eulerian trail)
- 오일러 경로(Eulerian trail)은 그래프에 존재하는 모든 Edge를 정확히 1번씩만 방문하는 연속된 경로이고, 이때 시작점과 도착점이 같다면 오일러 회로(Circuit)이 된다.
- 오일러 회로는 시작과 끝점을 제외하고는 들어오는 간선이 있다면, 반드시 나가는 간선이 하나 더 있어야 한다. 따라서 차수가 항상 짝수
- 오일러 경로는 무향 그래프일 경우 차수가 홀수인 정점이 2개일 때 존재
- 오일러 회로는 무향 그래프일 경우 차수가 홀수인 정점이 0개일 때 존재
- 오일러 회로 구하는 방법은 Hierholzer's 알고리즘과 DFS가 있다.
- 정점을 방문하면서 정점의 간선을 지우고, 차수를 1씩 줄여나감
- 해당 정점에 더이상 간선이 없는 순간 정점 번호를 출력하고 이어 붙인 것이 답
- 위 그림에서 A B C 방문하면 다음 방문지는 D, E, F가 될 수 있음
- D를 방문하는 경우 D-> A로 가서 A가 더이상 간선이 없어 방문이 끝나 C로 돌아오고 "A D"를 출력
- C로 돌아와서
D, E, F 에서 E를 방문하고 C E F C로 가면 C도 더이상 간선이 없으므로 "C E F C"를 출력하고 C에서도 시작점인 A로 돌아가 "B A"를 출력해 - 이어붙이면 " A D C E F C B A "
- D말고 E를 먼저 방문해도 결과는 같음
오일러 경로 - Hierholzer's
- 아무 정점 v에서 출발하여 v로 돌아오는 경로를 하나 뽑는다.
- 경로에 속한 정점 중 인접한 간선들 중 경로에 쓰이지 않은 간선이 있는 정점 u가 존재하면 u로 시작해 아직 방문하지 않은 간선만 사용해 u로 돌아오는 경로를 하나 더 찾아 원래 경로에 끼워 넣는다
오일러 경로 문제 - 프로그래머스 여행 경로
# 문제를 오일러 회로 구하는 방식으로 접근하여 Hierholzer's 알고리즘 사용
# DFS 스택? 으로도 볼 수 있나?
def solution(tickets):
routes = {}
for t in tickets:
routes[t[0]] = routes.get(t[0], []) + [t[1]]
for r in routes:
routes[r].sort(reverse=True)
stack = ["ICN"]
path = []
while len(stack) > 0:
top = stack[-1]
if top not in routes or len(routes[top]) == 0:
path.append(stack.pop())
else:
stack.append(routes[top][-1])
routes[top] = routes[top][:-1]
return path[::-1]
######################################################
from collections import defaultdict
def solution(tickets):
r = defaultdict(list)
for i,j in tickets:
r[i].append(j)
for i in r.keys():
r[i].sort()
s = ["ICN"]
p = []
while s:
q = s[-1]
if r[q] != []: # 위랑 차이점은 defaultdict를 써서 dest가 없는 노드라도 에러가 안난다는거
s.append(r[q].pop(0))
else:
# 다음 목적지가 없는데 티켓이 소진이 된 것이 아니라면 맨 마지막 dest일 것임
# 경로가 남은 곳 까지 pop해서 p에 넣으면 r[q]가 있는 곳으로 가게되고 남은 티켓을 소진하게 됨
p.append(s.pop())
return p[::-1]오일러 경로 문제 - 프로그래머스 방의 개수
from collections import defaultdict
def solution(arrows):
dx = [-1, -1, 0, 1, 1, 1, 0, -1]
dy = [0, 1, 1, 1, 0, -1, -1, -1]
graph = defaultdict(list)
x, y = (0, 0)
answer = 0
for d in arrows:
for _ in range(2):
nx, ny = x + dx[d], y + dy[d]
if (nx, ny) in graph and not (x, y) in graph[(nx, ny)]:
# 노드에 또 다시 방문했고,
# 이미 지나왔던 간선이 아니면
answer += 1
graph[(nx, ny)].append((x, y))
graph[(x, y)].append((nx, ny))
x, y = nx, ny
return answer
심화/기타 알고리즘
1. 투포인터(Sliding Window)
- 슬라이딩 윈도우라고도 함
- 리스트에 순차적으로 접근해야 할 때 두개의 점의 위치를 기록하면서 처리하는 알고리즘
- 우리가 2,3,4,5,6번 학생을 지목해야 할 때 2번부터 7번까지 학생이라고 함
- 이처럼 리스트에 담긴 데이터에 순차적으로 접근해야 할 때는 시작점과 끝점 2개의 점으로 접근할 데이터의 범위를 표현할 수 있다.
- 전체 값을 갱신하지 않고 이동한 왼쪽, 오른쪽 포인터의 값만 갱신하는 것이 포인트고 이 때문에 O(N)
- 크기가 고정일 때 슬라이딩 윈도우 투포인터 떠올리기
예제 : 특정한 합을 가지는 부분 연속 수열 찾기
- N개의 자연수로 구성된 수열이 있다.
- 이때 합이 M인 부분 연속 수열의 개수를 구해보시오. 제한 수행시간은 O(N)
- 완전탐색으로 푼다면 O(N * N)
- 문제 해결 아이디어
- 시작점과 끝점이 첫 번째 원소 인덱스 0을 가리키도록 한다
- 현재 부분 합이 M과 같다면, count += 1
- 현재 부분 합이 M보다 작다면, end += 1
- 현재 부분 합이 M보다 크다면, start += 1
- 모든 경우를 확인할 떄까지 2~4과정 반복
n, m = 5, 5
data = [1, 2, 3, 2, 5]
count = 0
interval_sum = 0
end = 0
for start in range(n):
while interval_sum < m and end < n:
interval_sum += data[end]
end += 1
if interval_sum == m:
print(f'{start}-{end - 1}')
count += 1
interval_sum -= data[start]
print(count)
- 문제
- 카카오엔프 기출 문자열의 다양성
- 백준 12891 : DNA 비밀번호
- 백준 2003 : 수들의 합
- 백준 1644 : 소수의 연속합
- 백준 1806 : 부분합
- 백준 2230 : 수 고르기
- 백준 1484 : 다이어트
- 백준 2038 : 골룽 수열
- 백준 2531 : 회전 초밥
- 백준 2096 : 내려가기
- 백준 2293 : 동전1
2. 구간 합(Interval Sum) 빠르게 계산
- 연속적으로 나열된 N개의 수가 있을 때 특정 구간의 모든 수를 합한 값을 계산하는 문제
- ex. 10, 20, 30, 40, 50 에서 2번재부터 4번째 수까지의 합은 20 + 30 + 40 = 90
- 구간 합 계산이 한번이라면 선형탐색하면 되는데, 여러번 이라면?
- 문제
- N개의 정수로 구성된 수열과 M개의 쿼리가 주어진다.
- 각 쿼리는 Left와 Right로 구성되어 있고 [Left, Right] 구간 합 출력
- 수행시간 O(N+M)
- N개의 정수로 구성된 수열과 M개의 쿼리가 주어진다.
- 해결 아이디어 : Prefix Sum(접두사 합)
- 배열의 맨 앞부터 특정 위치까지의 합을 미리 구해 놓은 것
- 알고리즘
- N개의 수 위치 각각에 대한 접두사 합을 계산해 P에 저장한다.
- 매 M개의 쿼리 정보를 확인할 때 구간 합은 P[Right] - P[Left - 1]이다.
- [10, 20, 30, 40, 50]
- P > [0, 10, 30, 60, 100, 150]
- Left=1, Right=3 > P[3] - P[0] = 60
n = 5
data = [10, 20, 30, 40, 50]
sum_value = 0
prefix_sum = 0
for i in data:
sum_value += i
prefix_sum.append(sum_value)
left, right = 3, 4
print(prefix_sum[right] - prefix_sum[left - 1])3. 소수 판별 알고리즘
- 약수의 대칭성을 이용하기 O(sqrt(x))
- 16의 약수는 1,2,4,8,16이고, 2*8=16, 8*2=16으로 대칭이다. (여기서 가운데 약수는 4이고 루트16이다.)
- 특정 자연수의 모든 약수를 찾을 때 가운데 약수(제곱근)까지만 확인하면 된다. 예를 들어, 16이 2로 나누어 떨어진다는 것은 8로도 나누어 떨어진다는 것을 의미.
import math
def is_prime(x):
for i in range(2, int(math.sqrt(x) + 1)):
if x % i == 0:
return False
return True
- 위 알고리즘은 1개의 수의 소수를 판별
- 특정 범위 안의 수에 존재하는 소수를 찾을 땐? > 에라토스테네스의 체
4. 에라토스테네스의 체
- 특정한 수의 범위 안에 존재하는 모든 소수를 찾을 때, 즉 다수의 자연수에 대해 소수 여부를 판별
- N보다 작거나 같은 모든 소수를 찾을 수 있다.
- 동작과정
- 2부터 N까지 모든 자연수를 나열
- 남은 수 중에서 아직 처리하지 않은 가장 작은 수 i를 찾는다.
- 남은 수 중에서 i의 배수를 모두 제거한다 (i는 제거하지 않는다)
- 더 이상 반복할 수 없을 때까지 2와 3을 반복한다.
- 시간 복잡도는 선형에 가까울 정도로 빠름 O(NloglogN)
- 하지만 메모리가 많이 필요하다
- 메모리를 줄여야 한다면
import math
n = 1000
array = [True for i in range(n + 1)]
for i in range(2, int(math.sqrt(n)) + 1):
if array[i] == True: # i가 남은 경우 = 소수
j = 2
while i * j <= n:
array[i * j] = False
j += 1
for i in range(2, n + 1):
if array[i]:
print(i, end=' ')5. 비트마스킹
- 정수의 이진수 표현을 자료 구조로 쓰는 알고리즘.
- 효율적인 집합 연산을 수행하거나 관리할 때 사용.
- ex. 부분 집합 생성 및 탐색, 조합 문제, 상태 압축
- bit 연산이기 때문에 시간 복잡도가 O(1)
- 비트연산자
- 1010 & 1111 = 1010 # AND 모두 1이면 1
- 1010 | 1111 = 1111 # OR 둘 중 하나라도 1이면 1
- 1010 ^ 1111 = 0101 # XOR 대응하는 비트가 서로 다르면 1
- ~1010 = 0101 # NOT 비트반전
- 1001 << 2 = 100100 # Left shift 왼쪽으로 2칸 밀고 0으로 채우기
- 1001은 10진수로 9, int("1001",2)=9 | A * 2^B
- 100100은 10진수로 36, int("100100",2)=36
- 1010 >> 2 = 0010 # Arithmetic Right shift
- 00000100 >> 1 = 00000010 (4 >> 1 = 2) | A * 2^B
- 11111111 >> 2 = 10011111 (-1 >> 2 = -31)
- 파이썬으로 비트표현
# 1. 0b 접두사 붙이기
num = 0b1010 # 앞의 0은 생략 00000000 00000000 00000000 00001010
# 2. bin() 사용
num = bin(10) # '0b1010'
# 2진수 > 10진수
num = int('00001010', 2)
# str을 이진수로
s = '0100'
bin(int(s, 2))- 비트연산
S = 122 # 0b1111010
idx = 2 # 0b1111'0'10
# 1. ADD : 2진수 숫자 S의 idx에 1을 추가
# 1 << idx : 1을 idx만큼 left shift 00000001 << 2 = 00000100
# 즉, idx자리만 1인 비트 만듬
bin(S | (1 << idx)) # 01111'0'10 | 00000'1'00 = 01111110
# 2. REMOVE : 2진수 숫자 S의 idx에 1을 제거
# 1 << idx idx자리만 1인 비트 만들고 not을 하면 idx자리만 0인 비트
# and하면 idx 값만 무조건 0이되고 나머지는 S자신 그대로
bin(S & ~(1 << idx)) # 01111'0'10 & 11111'0'11 = 01111010
# 3. CHECK : idx 값 확인
# 1 << idx idx자리만 1인 비트 만들고
# and하면 idx자리만 자기 자신이고 나머지는 모두 0
(S & (1 << idx)) # 01111'0'10 & 00000'1'00 = 00000000 # False = 0
idx2=1
(S & (1 << idx2)) # 011110'1'0 & 000000'1'0 = 00000010 # True = 1
# 4. Toggle : idx 값을 toggle(1이면 0, 0이면 1로 변환)
# 0과 XOR 연산하면 자기자신, 1과 XOR 연산하면 자신이 1이면 0, 0이면 1인 것 이용
bin(S ^ 1 << idx) # 01111'0'10 ^ 00000'1'00 = 01111110
# NOT 연산을 하면 부호비트까지 바뀌는거 처리해줘야해서 XOR 사용하는 것이 좋음
binary_string = "010100"
# 문자열을 정수로 변환
num = int(binary_string, 2)
# 모든 비트를 1로 만드는 마스크 생성 (ex. '010100'의 길이만큼)
mask = (1 << len(binary_string)) - 1
# XOR 연산으로 비트를 반전
inverted_num = num ^ mask
# 다시 2진수 문자열로 변환
inverted_string = bin(inverted_num)[2:].zfill(len(binary_string))
print(inverted_string) # 출력: 101011
# S를 -1로 초기화하면 모든 비트가 1, S = -0b1
# S를 0으로 초기화하면 모든 비트가 0, S = 0b0
bin(-0b1 & 0b0) # '0b0'
bin(-0b1 | 0b0) # '-0b1'최애 유형은 비트마스킹이랑 DP
추천 문제
| 문제 | 유형 |
| 124나라의숫자 | 수학 (삼진법 |
| 최고의 집합 | 수학 |
| 디스크 컨트롤러 | 우선순위 큐 |
| 여행경로 | 그래프 - 오일러, DFS |
| 순위 | 그래프 - 플로이드 워셜 |
| 퍼즐 조각 채우기 | 구현 - BFS |
| 아이템 줍기 | 구현 - BFS |
| 징검다리 건너기 | 이진탐색, 우선순위 큐 |
| 가장 긴 증가하는 부분 수열 5 | 이진탐색 |
| 방의 개수 | 그래프 - 오일러 |
| 사칙연산 | DP |
| 평범한 배낭2 | DP |
| 파일 합치기 | DP - Knuth's optimize |
| 조이스틱 | 그리디 |
| 큰수 만들기 | 그리디 |
| 섬 연결하기 | 그리디 - 크루스칼, 프림 |
| 단속카메라 | 그리디 |
| 징검다리 | 이분탐색 |
| 젼력망을 둘로 나누기 | BFS |
| 백준4195 | UnionFind |
| 신촌통폐합계획 | LinkedList |
| 통신망분석 | UnionFind, BFS |
| 코드트리투어 | |
| 어항정리 | 빡구현 |
| 도넛과막대그래프 | 그래프 |
| 소문난 칠공주 | BFS, DFS, 백트래킹 |
| N-Queen | 백트래킹 |
'SW 개발' 카테고리의 다른 글
| Python vs PyPy (0) | 2025.11.16 |
|---|---|
| [Cursor] 커서로 Slack 액션 아이템 생성 봇(feat.llm) 만든 후기 (0) | 2025.03.26 |
| 알고리즘 공부 - 파이썬 (0) | 2025.01.15 |
| [개발자 상식] 개발자가 되기 위한 첫 걸음을 떼어줄 책 (1) | 2023.03.15 |
| [Node.js로 서버 만들기] 책을 출간하였습니다. (0) | 2021.12.19 |
Contents
소중한 공감 감사합니다