자연어 NLP
[NLP] Large Language Diffusion Models (LLaDA)
Large Language Diffusion Models
link : https://arxiv.org/pdf/2502.09992
Overview
기존 대부분의 LLM은 Autoregressive 방식을 따른다. 즉, 주어진 이전 토큰들을 기반으로 다음 토큰을 순차적으로 예측하며 문장을 생성하는 방식이다.
이 논문의 저자들은 LLM의 핵심 능력은 Autoregressive 구조에만 의존하지 않으며 다른 생성 방식으로도 기존 SOTA LLM에 필적하는 성능을 낼 수 있다고 주장한다. 이에 따라 저자들은 새로운 접근 방식인 LLaDA (Large Language Diffusion Models)를 제안한다.
LLaDA는 전체 문장을 순차적으로 예측하지 않고,
일부분이 마스킹된 토큰 시퀀스를 입력으로 받아
마스킹된 토큰을 확산 복원하는 방식으로 동시에 예측하는 비순차적 언어 생성 모델 아키텍처이다.
Introduction
Is the autoregressive paradigm the only viable path
to achieving the intelligence exhibited by LLMs?
→ Not a simple "yes"
먼저 저자들은 Autoregressive 방식이 LLM을 학습하는 유일한 길이 아니고
MLE 기반 확산 모델링 방식을 따르면서 충분한 규모와 구조적 개선만 갖춘다면 확산 기반 모델도 충분한 대안이 될 수 있다고 주장한다.
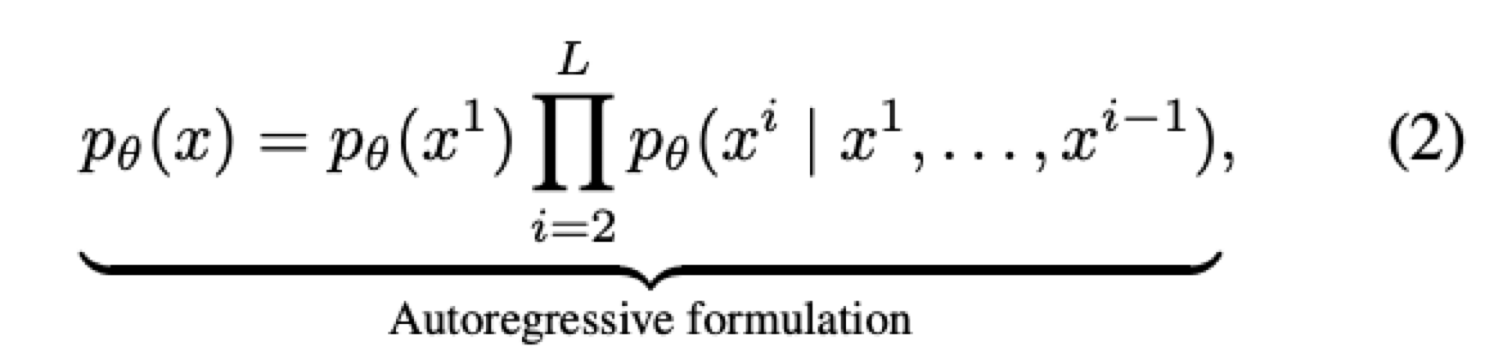
수식(1)은 Generative modeling principles, 즉 언어 모델 학습 본질적 원리를 수식화한 것이다. 대부분의 확률 생성 모델은 이 학습하려는 분포 p를 데이터 분포 q에 가깝게 만드는 MLE(Maximum likelihood)로 학습을 하게 된다.
(2)는 GPT 계열 모델들이 사용하는 Autoregressive factorization으로
전체 문장의 확률은 각 토큰을 앞에서부터 하나씩 예측한 확률의 곱으로 모델링하고 이를 통해 토큰을 순차적으로 예측한다.
저자들은 LLM의 핵심 능력은 (2) Autoregressive factorization 방식이 아니라 (1) Generative modeling principles이 핵심 원리라고 주장한다. Autoregressive Model(ARM)은 일종의 구현 방식일 뿐이며 LLM 능력의 핵심은 토큰을 잘 복원하도록 학습된 확률 생성 모델이어야 한다는 것이다.
또한 LLM의 일부 근본적 한계 역시 이 AR 방식에서 기인한 것이라고 한다.
1. 비효율적인 샘플링
한 토큰씩 왼→오 방향으로 순차 생성해야 하므로 병렬화가 어려움
2. Unidirectional context
앞 쪽 토큰만 조건으로 사용 → 양방향 정보 활용 불가
3. Reversal curse
A→B는 잘 배워도 B→A는 못배움 (비대칭적 생성 구조)
4. 정보 지연
중요한 정보가 뒤에 나오면 늦게야 반영 가능
LLM Capabilities
LLM의 scalability, instruction-following, in-context learning은 ARM의 고유 결과가 아니라 더 일반적인 확률 생성 모델링(generative modeling)의 결과라고 하며 이에 대한 약한 설득에 관한 내용이다
1. LLM Scalability
모델 규모가 커질수록 성능이 올라가는 현상은 Transformer 구조와 대규모 데이터와 모델 크기, 그리고 수식(1)의 생성 모델 원리간 상호작용으로부터 생긴다. 따라서 이 확장성은 ARM의 고유한 특성이 아니다. 그리고 여기서 Fisher consistency에 대해 언급하는데, Fisher consistency는 정답분포 q에 대해 MLE를 반복하면 정확한 분포로 수렴하는 특성을 말한다. 이상적인 조건에서 실제 분포를 복원할 수 있는 이론적 성질도 MLE 기반으로 한다. 즉, MLE 기반 확률 생성 모델은 모델만 충분히 expressive하다면 점점 정확해질 수 있다.
2. Diffusion Transformer
Diffusion Transformer가 비전 분야에서 성공한 사실은 ARM 없이도 확장성과 생성 능력을 확보한다는 실증적 근거가 된다고 주장
3. Instruction-following, In-context learning
LLM의 Instruction-following, In-context learning능력은 단지 GPT 계열 모델의 ARM의 결과가 아니라, 조건부 생성 모델이라면 (예: prompt → response 구조), 충분히 실현할 수 있는 일반적인 능력이다. 특히 언어 구조가 일관성 있게 주어지는 경우 (예: instruction → response)라면 diffusion 기반 모델도 이런 능력을 학습할 수 있다고 주장한다.
예를 들어 ARM은 이전 token이 condition된 확률곱으로 모델링하거나 diffusion은 전체 x를 점진적으로 마스킹하고 condition을 고정한 채 복원하는 형태로 학습할 수 있다. 이렇게 함으로써 일반 Text task와 같이 입출력 구조가 논리적으로 잘 정의되어 있기만 하면 Diffusion도 instruction-following을 충분히 학습할 수 있다.
4. Data Compressor
정보이론에 따르면 확률p가 클수록 그 시퀀스를 더 짧은 코드로 압축할 수 있는데 그렇기 때문에 ARM형태로 학습된 언어 모델의 확률 분포로 인해 GPT는 주어진 시퀀스에 대해 최적의 압축 방식을 학습한 것처럼 동작하게 된다. 실제로 데이터 압축키에 GPT를 활용한다고 한다. 하지만 이것도 충분히 expressive한 생성 모델이라면 ARM이 아니더라도 비슷한 정보 압축 성능을 낼 수 있다고 저자들은 말하고 있다.
LLaDA (Large Language Diffusion with mAsking)
예시 비교
Autoregressive
입력: [BOS] 토큰1 토큰2 토큰3 ...
출력: 토큰1 토큰2 토큰3 토큰4 ...
Step 0: [BOS]
↓
Step 1: [BOS] → The
↓
Step 2: [BOS] The → cat
↓
Step 3: [BOS] The cat → is
↓
...
학습: p(x) = p(x₁) · p(x₂|x₁) · p(x₃|x₁,x₂) · ...
(왼쪽 → 오른쪽 순차 생성)
샘플링: 각 단계에서 직전까지의 결과만 보고 다음 토큰 생성
LLaDA
입력: [Q: ...? A: [MASK] [MASK] [MASK] [MASK]]
초기 상태: [MASK] [MASK] [MASK] [MASK]
Step 1: [MASK] [MASK] [MASK] [MASK]
↓ ↓ ↓ ↓
Step 2: The [MASK] is [MASK]
↓ ↓ ↓ ↓
Step 3: The cat is cute
학습: 원래 답변 텍스트를 점진적으로 마스킹 → 복원 학습
q(x^t | x^0), p_θ(x^{t-1} | x^t)
샘플링: 모든 토큰을 [MASK]로 시작 → 한꺼번에 예측 & 반복 복원
Diffusion foward process
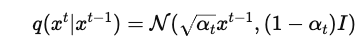
Diffusion reverse process
기존 Diffusion model은 continous 데이터 값에 Gaussian noise를 점진적으로 추가하고 이 노이즈를 제거하는 디노이징 프로세스를 학습하였다면,
Text에서는 연속 값 노이즈가 아닌 이산적 마스킹이므로 continuous 대신 discrete 확산 구조가 필요하다.
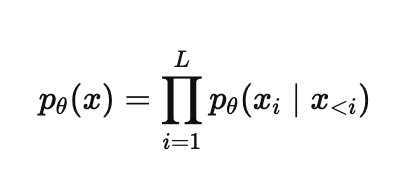
기존 ARM은 위와 같이 문장 확률을 분해하여 학습하게 된다. 반면 LLaDA는 forward process와 reverse process를 통해 분포 $p_{\theta} (x^0)$를 정의하며, 이는 확률 생성 모델의 일반 원리에 충실한 방법이다.
Forward Process
forward process과정은 discrete diffusion에서 노이즈를 추가하는 과정을 의미한다.
$x^0 \sim p_{data}(x^0)$ 에서 시작해, $ t \in [0, 1]$에 걸쳐 각 토큰이 독립적으로 마스킹된다.
각 토큰이 시간 $t$에 마스킹될 확률은 $t$이고, 마스킹되지 않을 확률은 $1-t$이다.
$t=1$일 때는 모든 토큰이 완전히 마스킹된 상태이다.
Reverse Process
forward과정에서 얻은 $x^t$에서 mask predictor 모델 $p_{\theta}(x^0 | x^t)$를 사용해서 마스킹된 위치의 원래 토큰을 예측한다.
이 과정은 $t=1$인 상태 즉 모든 토큰이 Masking된 상태에서 $t=0$ 마스킹된 토큰이 모두 없이 온전한 토큰이 남은상태로 시간 역방향으로 반복 수행되어 원본 문장을 복원한다.
Objective
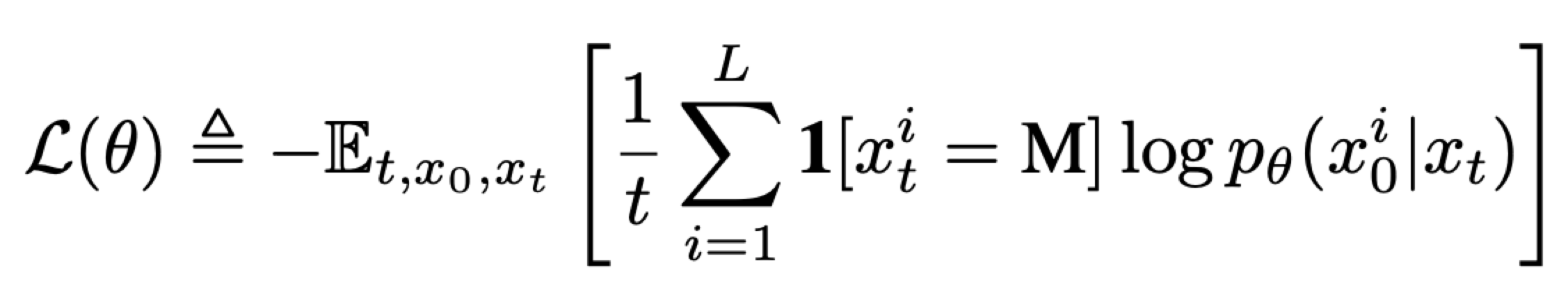
- $t \sim U[0,1]$: 마스킹될 확률이자 시점 $t$는 Uniform 분포에서 샘플링
- $x^0$: 원본 시퀀스
- $x^t$: forward process에서 나온 Masking sequence
- $\mathbf{1}[x_{i}^{t} = M]$: i번째 토큰이 마스킹된 경우만 Loss 계산
- $\frac{1}{t}$: 마스킹 비율을 보정하는 정규화 항
- $p(x_{i}^{0}|x^t , t)$: $x^t$와 시점 t를 받아 모델이 i번째 토큰에 대해 예측한 확률 분포 중 정답 토큰 $x_i^0$에 할당한 확률
- $-\log {p(x_i^0 | x^t, t)}$: i번째 토큰에 대해 모델의 예측이 정답과 얼마나 차이가 나는지 측정하는 -log likelihood
이는 masked tokens에 대한 cross-entropy 평균 값을 의미하게 되고 기존 log likelihood($-\log{p}$)의 upper bound이다.
*보충 설명 ------------------------
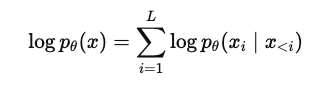
일반적인 ARM은 수식 (2)와 같이 factorized된 확률을 학습한다. 이 구주로 인해 각 토큰의 조건부 확률을 차례로 계산할 수 있다. 이걸 그대로 평균을 내면 MLE loss가 된다.
하지만 LLaDA는 AR 구조가 아니기 때문에 입력 전체를 mask로 만들고 한꺼번에 masked token을 복원하는 방식이 된다.
즉, 한 스텝에서 마스킹된 토큰을 '독립적'으로 복원하게 된다.
이 구조에서는 fully unmasked 샘플의 로그 확률 $\log{p_{\theta}(x_0)}$을 직접적으로 계산할 수 없다.
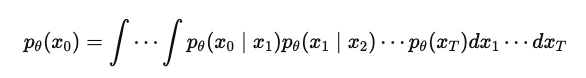
$p_{\theta}(x_0)$은 여러 스텝에 걸쳐 Reverse diffusion process를 거쳐야 정의되는데
이 과정은 복잡한 markov process이다.
이 적분은 closed-form이 아니며 계산이 불가능하기 때문에 직접적으로 MLE 학습이 불가하기 때문에,
MLE의 upper bound를 최소화하는 surrogate objective를 사용해야 한다.
따라서 DDPM(Denoising Diffusion Probabilistic Models)에서 유도된 것과 유사하게 variation 방식을 사용하게 된다.
DDPM 논문처럼 forward $q(x_t|x_0)$과 reverse $p_{\theta}(x_0 | x_t)$사이의 evidence lower bound(ELBO)를 설정할 수 있다.
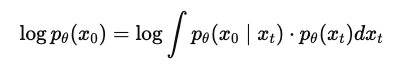
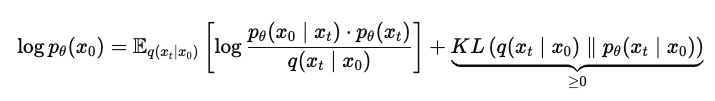
중간 variable $x_t$ (forward process로부터 얻은 noised sequence)를 사용해 log p를 위와 같이 정의한다.
우리가 모르는 $p_{\theta}(x_t)$ 대신 foward process에서 정의한 $q(x_t|x_0)$을 사용하여 정리하면
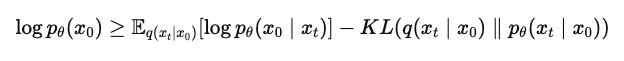
다음과 같은 upper bound를 정의할 수 있다.
forward와 reverse 간 KL이 작아야 bound가 tight하다는 것을 이용해 surrogate loss로 $\mathbb{E}_{t, x_t}[-\log{p_{\theta}(x_0|x_t)}]$를 사용한다.
또한 surrogate loss에서 어떤 시간 t와 그에 대응하는 masked sequence x_t를 모든 경우에 대해 평균하는 것은 불가능하기 때문에
Monte carlo 방법을 사용해 기대값을 샘플 평균으로 대체하여 objective를 최적화 한다.
*-------------------------------
이를 통해 LLaDA는 MLE와 같은 Generative modeling principles 기반하여 학습할 수 있게 된다.
또한 마스킹된 위치를 복원하는 과정은 좌우 문맥을 모두 사용하므로 자연스럽고 일관된 문장 생성이 가능하다고 얘기한다
A Conceptual Overview of LLaDA
위에서 설명한 Objective를 최적화하여 LLM을 학습하는 것이 (a)Pretraining 단계이다.
Pretraining 후 (b)SFT 단계를 거치게 되는데 기존 LLM 학습과 유사한 방식으로 적용할 수 있으며 Diffusion 구조에서도 완전히 호환될 수 있다.
Pretraining 단계에서는 무작위 텍스트 복원 학습이기 때문에 $p_{\theta}(x_0)$을 학습하지만 SFT prompt가 주어지면 response를 학습하도록 하는 조건부 분포 학습이라는 점만 다르다.
prompt $p_0$는 그대로 두고 response $r_0$을 마스킹하여 $r_t$로 만든다. 그리고 $p_0$와 $r_t$를 모델에 입력한 후 $r_0$에서 마스킹된 부분을 복원하여 Loss를 계산한다.
즉 SFT는 Pretraining과 구조적으로는 완전히 동일하고 단지 마스킹된 Response 부분에만 집중되었다는 점만 다르다.
(c)Inference는 prompt $p_0$는 고정으로 두고 $r_0$은 길이 L만큼 즉 L개의 토큰을 모두 마스킹한 상태에서 시작한다.
L과 sampling steps(denoise steps) 수 N은 모두 하이퍼파라미터 이다. 즉 응답을 '얼마나 길게' 생성할지 '몇 단계에 걸쳐 복원'할 지 사용자가 미리 정해야 한다.
그래도 eos 토큰 같은 게 생성되고 이를 지워서 토큰 길이는 동적으로 조절할 수 있는 것 같다. 단, L보다 더 긴 답변은 생성할 수 없을 것이다.
Inference (reverse process)에 대해 좀 더 자세히 보면 t는 [0,1]이기 때문에 스텝 수로 나눠 t를 설정한다. ex) t=1.0,0.9375,0.875,…,1
4라인: 현재 마스킹된 시퀀스 r_t에 대해 모든 마스크 토큰을 예측한다. mask predictor가 각 위치에 가장 확률 높은 토큰을 골라 시퀀스 r_0을 생성하게 된다.(Greedy decoding)
9라인: 복원된 토큰이라도 일정 확률로 다시 마스킹하게 되는데 이로 인해 샘플링을 안정적으로 하는 효과를 주는 것 같다.
prob을 s/t로 맞추는 것은 만약 현재 스텝에서 복원된 토큰이 0.75이고 다음 스텝의 t가 0.8이면 토큰을 다시 80%로 마스킹되도록 맞춰주는 것이다.
Re-masking strategy
알고리즘4의 9라인에서 랜덤으로 리마스킹하는 것이 아니고 이는 low-confidence 토큰만 다시 마스킹하는 deterministric re-masking 기법을 추가한 inference 알고리즘이다.
13라인: 모든 토큰을 다시 순회하여
14라인: confidence가 가장 낮은 $n_{un}$개의 토큰에 해당하면
15라인: re-masking
cofidence를 추가로 계산해야 한다는 단점은 있지만 실용적이고 더 정교하게 inference step을 조절할 수 있게 된다.
이 외 Semi-autoregressive remasking 전략도 소개하는데
시퀀스를 여러 블록으로 나누고 각 블록은 디퓨전 방식으로 생성하되 블록끼리는 좌 -> 우 방향으로 생성하는 기법이다.
이렇게 함으로써 AR의 장점을 가져가겠다는 전략같다.
Experiments
autoregressive 없이도 sota급 llm 능력을 달성할 수 있음을 보여주는 실험
MMLU, GSM8K 등에서 FLOPs 대비 ARM 기반 모델과 거의 동일하거나 나은 성능 곡선을 보여준다.
여기서 CMMLU만 중국어 벤치마크 데이이터셋이다.
LLaDA는 대부분의 벤치마크에서 FLOPs에 따라 성능이 ARM과 거의 유사한 곡선을 따라가며 확장된다. 이는 디퓨전 기반 모델도 LLM처럼 스케일할 수 있다는 실험적 증거라고 볼 수 있다.
작은 모델에서는 LLaDA가 약간 열세이지만 모델이 커질수록 성능차이가 감소하는 걸 볼 수 있다.
특히 이 실험의 벤치마크들은 고난이도 벤치마크이고 baseline 모델들은 sota급 모델(llama, qwen 등)이다.
이 실험이 말하고자 하는 바는 "LLaDA는 autoregressive 없이도 확률 생성 원리(MLE)에 충실하게 학습하면, 동일한 계산량에서 ARM 기반 LLM과 동등한 성능을 낼 수 있다."는 것이다.
reversal reasoning능력에서 gpt-4o초과 달성한 걸 보여준 실험
순방향 역방향 문장 모두 학습한 후, 역방향 문장 재구성 성능(reversal reasoning)을 측정한 것이다. LLaDA는 GPT-4o, GPT-4-turbo보다도 reversal task에서 더 우수한 성능을 보였다. 이 벤치마크는 중국어 시(poem) 기반 단문에서 역방향 완성 과제를 수행한 결과이며, LLaDA‑8B는 GPT‑4o 대비 약 +8.1%p 향상 된 성능을 기록했다. 이 실험 결과는 일반 ARM 구조가 잘 못하는 대표적 약점 (reversal curse)을 LLaDA는 해결할 수 있다는 것을 보여줬다고 주장한다. 즉 LLaDA는 전체 문장을 마스킹 후 양방향 복원하므로, 방향 비대칭 문제를 해소했다고 주장한 것이다.
Contribution
- 기본 ARM의 대안 제시 : 확산 모델로도 LLM 핵심 능력 실현가능
- 이산 공간에서의 확산 : 이산 토큰 공간에서의 마스킹 확산이라는 새로운 추론 전략 제시
- Re-masking 전략 : 문장 전반의 일관성과 자연스러움 향상
- 양방향 생성 : 문맥 이해, self-correction 가능
- 병렬화, 낮은 latency : 실시간 애플리케이션에 적합 (Gemini Diffusion)
- Reversal curse 극복 : 역추론 과제에서 뛰어난 성능
Review
이 논문은 ICML에 최종적으로 Reject되었는데 리뷰어들의 의견을 살펴보면,
- 기존 Masked diffusion, discrete diffusion모델을 그대로 가져와 확장한 것일 뿐이고 구조적 혁신이나 새로운 학습전략은 없었다.
- 일부 주요 결과를 보면 Sem-autoregressive 방식에서 성능이 좋은데 이는 AR을 완전히 대체할 수 있다는 주장과 모순됨.
- 또한 디퓨전 디노이징 스텝 Inference는 autoregressive KV caching 적용한 것보다 훨씬 느릴 것이라 예상할 수 있는데 이에 대한 효율성을 분석한 내용이 전혀 없음
특히 이 논문은 모델과 학습 코드가 공개되지 않아 재현이 어렵고 diffusion 계열 모델의 약점인 Inference 효율성에 대한 실험 근거가 부족하다는 점이 치명적이었을 것 같다. 특히 양방향 문맥을 고려할 수 있다는 reversal reasoning task에서도 중국어 기반 단일 태스크에 국한되어 일반화에 한계가 있다. 실험이나 논문의 수학적 표현 등은 설득력이 있지만 전체적인 논문 설득의 구조가 이해하기 어렵고 복잡하지만 이를 설득하는 근거들이 모두 약한 것 같다.
그래도 diffusion 기반 언어 모델인 LLaDA를 8B 규모로 확장하고, autoregressive 모델과의 비교를 통해 diffusion 방식의 가능성을 실증했다는 점에서 의미가 있다. 특히 instruction-following, reversal reasoning, infilling 등의 핵심 능력을 diffusion 모델로 구현한 점은 인상적이다. 최근 Gemini-Diffusion 등과 함께 diffusion LLM의 실현 가능성을 보여준 초기 사례 중 하나로 볼 수 있다.
현재까지 발전된 Diffusion 계열 LLM은 block 단위 병렬 생성, few-step sampling(distillation 기반), KV 캐시 유사 구조 등을 활용해 속도를 크게 향상시켜, 기존 diffusion 모델의 느린 샘플링 한계를 극복하고 autoregressive 모델에 근접한 실시간 생성 성능을 달성하고 있다
'자연어 NLP' 카테고리의 다른 글
Contents
소중한 공감 감사합니다