[RLHF] DPO: Direct Preference Optimization, DPO

Direct Preference Optimization: Your Language Model is Secretly a Reward Model

 

Link : https://arxiv.org/pdf/2305.18290.pdf

 

 

Neurips 2023 논문이고, 이전 RLHF 방법론들에서 Reward model을 학습시키는 과정을 없애므로써, 기존의 RLHF 방법들의 복잡한 학습 파이프라인을 simple relative cross entropy training 으로 바꾼 논문.

 

Instruct gpt의 선호도 데이터셋은 openai에서 공개했지만 reward model은 공개하지 않았고 hugging face에 올라온 많은 reward model도 아직까지는 작은 규모의 연구 집단에서 사용하기에 썩 유용해 보이지 않는다. 따라서 고성능의 reward model을 사용할 수 없는 곳에서 RLHF를 하려거든 DPO는 매력적인 옵션이 될 것이다.

 

 

✲ Introduction

 

LM을 human preference에 따른 goal, priorties, skillset 등으로 만들어진 데이터에 tuning하고 싶을 때, 우리는 모델이 잘 하는 것만 imitate하길 바란다. 사람이 annotate한 데이터셋이라면, 평균적으로 반이상은 보통 능력의 데이터셋일 것이고 많아봐야 50%정도가 좋은 퀄리티의 데이터셋일 수 있다. 우리는 LM을 학습시키면서 LM이 데이터셋의 퀄리티까지 구별해서 좋은 퀄리티의 데이터셋 쪽으로 학습하길 원한다.

 

하지만 LM training 은 dataset maximum likelihood로 학습되므로, desired response, behavior를 잘 선택하여 모델에게 입력해주어야 똑똑한 LM이 학습될 수 있다. 따라서 데이터셋 이상의 능력을 가진 LM을 학습시키려면 RL-based approach를 사용하는 것은 필수라고 볼 수 있다.

 

기존 RL 방법들은 preference dataset으로 리워드 모델(RM)을 fitting해야 해서 학습 파이프라인이 매우복잡했다. DPO는 RL objective를 간단한 bionary cross entopy object로 풀어서 preference learning 파이프라인을 단순화 시킨데 의의가 있다. RLHF를 위해 즉 RM을 없애고 objective를 단순화한 것이 contribution이라고 할 수 있다.

 

 

 

왼쪽 그림은 이전까지 대부분의 RLHF 알고리즘들의 training phrase이고, 오른쪽은 DPO의 학습과정이다. 이전 RLHF가 pre-trained LM(가능하면 supervised fine tuning까지 거친)이 데이터셋 2개 혹은 그 이상을 생성하고 사람이 순위를 매긴 후, 순위가 매겨진 데이터셋에 preference loss로 Reward Model(RM)을 학습한 뒤, KL-constrained RL 학습 즉 RL-tuning 단계를 거친다. 다시 정리해보자면 크게 3단계가 필요하다는 것이다.

 

1) LM pretraining + LM task-specific supervised fine-tuning(optional)

2) data annotation by human + Reward Model training

3) RL-tuning

 

하지만 DPO는 여기서 Reward model 단계를 없애고 선호도 데이터셋만 있다면, relative log probability를 증가하는 objective로 LM을 tuning할 수 있다. 어쨌던 사람이 생성했던, 자동으로 라벨링 된 것이던, classifier 등을 이용했던, 선호도 데이터셋이 필요한 건 맞으나 애초에 RLHF의 발전은 relative preference labeling이 상대적으로 더 쉽다는 것을 이용하기 때문에 선호도 데이터셋을 이용한다는 것은 큰 단점이 아닐 것이다. 하지만 선호도 데이터셋이 충분해서 고퀄리티의 Reward model을 학습시킬 수 있으면 사실 reward model을 학습시키는 것이 더 좋을 수도 있다.

 

Reward model을 잘 학습해놓으면 새로 들어오는 데이터셋에 대해서도 선호도 라벨링이 가능하기 때문이다. 하지만 첫 부분에 언급했듯 아직까지 꽤나 성능 좋은 reward model을 일반 사람들이 접근하기는 어려워보인다. 그래서 DPO가 주목받지 않았나도 싶다. DPO는 reward model 학습이나, 학습동안 policy에서 샘플링하는 것 없이 simple binary cross entropy loss하나로 policy를 optimize할 수 있기 때문이다.

 

 

 

✲ Preliminaries

 

DPO 설명하기 앞서 이전 RLHF pipeline에 대해 알아보자.

 

1) SFT phrase

 

generic pre-trained LM이 있으면 여기서 특정 task에 대한 데이터셋으로 MLE supervised finie-tuning하는 단계 이 단계에서$\pi^{SFT}$를 얻게된다.

 

 

2) Reward Modeling Phrase

 

 

 

1단계에서 얻은 $\pi^{SFT}$에서 prompt $x$를 넣고 $y$ 2개를 생성하고 human labeler가 더 선호하는 쪽을 $y_w$, 덜 선호하는 쪽을 $y_l$라고 라벨링한다. 그리고 human preference probability를 위해 각 pair에 대한 선호가 있을 때 전체 선호도를 모델링할 수 있는 Bradley-Terry모델을 주로 사용하게 된다(1). 그리고 $y_w$, $y_l$이 있을 때 negative log-likelihood로 Reward Model을 학습시킨다.(2). 

 

 

3) RL Fine-tuning Phrase

 

 

RL 튜닝  단계에서 KL-constrained Reward maximization objective (3)을 통해 policy optimization을 풀게 된다. 맨 아랫줄 처럼 리워드를 리워드 모델에서나온 값 빼기 KL penalty로 정의하고, RL 알고리즘을 사용해 이 reward를 maximization하는 policy를 찾게되는데 주로 PPO를 사용한다. 이러한 비슷한 방법들 대부분은 KL term을 이용해 reference model과 policy를 너무 멀어지지 않게 함으로써 높은 리워드를 받지만 fluency를 잃지 않도록 한다.

 

 

 

✲ Direct Preference Optimization

 

 

 

해당 논문에서는 RL policy를 optimization하기 위해 사용했던 KL-conatrained RL objective (3)을 아래와 같은 objective로 바꿔주고,

 

 

 

이에 대한 전개는 아래와 같다.

 

 

 

먼저 (11) 식의 KL-constrained RL obejctive에서 KL텀을 풀어서 써주고 (1번째 줄),
$x-1/\beta$를 해주면 2번째 줄처럼 식이 전개가 되고, 2번째 줄 식에서 log로 묶어주고 $\log Z(x) - \log Z(x)$를 해주고, 잘 정리해주면 (12)와 같은 식이 나온다. 단순히 log exp 성질만 이용하면 풀어쓸 수있다. 

 

 

 

그리고 $Z(x)$가 $\pi_{ref}(y|x) \exp(\frac{1}{\beta} r(x,y))$에서 모든 가능한 y의 summation인 partition function $Z(x)$가 되면, (12)식에서 첫번째 텀의 분모는 probability distribution이 되고, 이를 $\pi^*$로 정의해본다. 이때 $Z(x)$는 오직 x와 $\pi_{ref}$에만 depend하고 $\pi$에는 depend 하지 않는다. 

 

 

 

정의한 $y^*$을 (12)에 대입해하면 (13)식처럼 정리할 수 있고 앞 부분은 $\pi$와 $\pi^*$의 KL divergence 가 된다. 해당 objective는 $\pi$와 $\pi^*$이 같을 때 KL이 0인 optimal solution을 가지므로, 따라서 우리가 구하고자하는 policy $\pi$는 (15)식과 같이 나타낼 수 있고 처음에 언급한대로 KL-constrained RL objective는 $\pi$가 (15)식일 때와 같다고 볼 수 있다.

 

 

우리가 ground-truth reward에 접근할 수 있다 하더라도, $Z(x)$를 구하는 것은 여전히 높은 cost를 가지므로, (1)번식 preference probability $p(y_w > y_l | x)$에서 reward $(r(x,y))$ 부분을 없이고 더 나아가 $Z(x)$를 구하지 않는 objective로 유도할 것이다.

 

 

 

일단 우리가 구했던 식 (4)에 양변에 log를 취하면 $r(x,y)$를 (5)식과 같은 꼴로 나타낼 수 있게 된다. 그리고 이렇게 구한 $r(x,y)$를 (1) 번식에 대입해서 아래와 같이 전개할 수 있다.

 

 

 

식 (16)이 기존 bradley-terry model이고, 여기에 (5),(17) 식의 $r(x,y)$를 대입해서 $\exp^{(a+b)} = \exp^a * \exp^b$ 성질을 이용해 $\beta \log Z(x)$를 소거해주고, $\beta \log \pi^*(y_1|x) / \pi_{ref}(y_1|x)$를 분모 분자에 나눠주면 두번째 줄로 전개할 수 있고 이는 sigmoid 식으로 유도가 되므로 가장 아랫줄의 식으로 정리해서 쓸 수 있다.

 

Bradley-terry 모델은 두 쌍에 대한 비교이고, 이를 K개 쌍에 대한 비교로 일반화한 모델을 Plackett-Luce model이라고 하며 Plackett-Luce model에서도 똑같이 $r^*$을 Plackett-Luce model에 대입해서 전개하면 

 

 

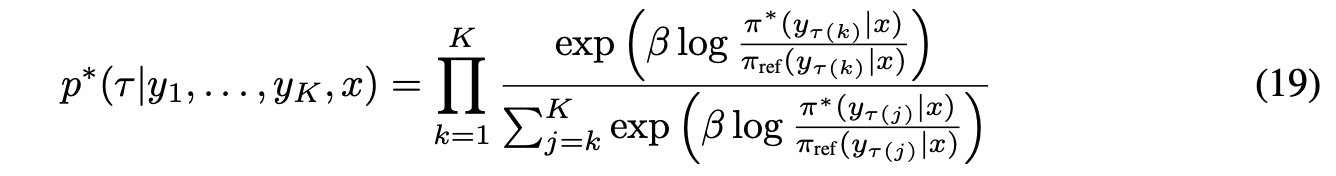
이처럼 비슷하게 $r(x,y)$와 $Z(x)$ 텀을 지워버릴 수 있다.

 

 

이전 RLHF에서 preference model을 위해 두 라벨의 log prob의 차이를 maximize하는 objective를 사용했던 것과 마찬가지로 DPO에서도 relative log likelihood objective로 최종 loss를 정의한다.

 

 

 

 

그리고 저자들은 이렇게 유도한 DPO objective에 gradient에 대한 anlaysis를 하는데,

 

 

$L_{DPO}$에 theta에 대한 gradient를 취하면, 선호한 라벨에 대한 log likeihood는 높이고, 선호하지 않은 likelihood는 낮추는 동시에 리워드가 잘못 estimate되면 큰 penalty를 주는 것 처럼 보인다. 이 텀이 reward estimate에 대한 weight가 된다고 저자들은 말하고 이 텀이 없는 경우 LM의 성능이 degenerate된다고 한다.

 

 

 

맨 마지막 처럼 $\beta \log \pi_{\theta} / \pi_{ref}$를 위 $r_{\theta}$로 치환해서, reward estimate에 대한 weight로 바꾼 것인데, 어떻게 reward를 policy와 reference policy의 ratio로 볼 수 있는지에 대한 theorem은 다음 단락에서 나온다.

 

 

 

✲ Theoretical Analysis of DPO

 

해당 섹션에서 DPO가 KL-constrained RL objective에서 유도된 optimal policy (4)번 식이 Bradley-terry 모델을 policy, reference policy ratio로 표현될 수 있는 reward function과 같다는 것을 보인다. 

 

 

 

먼저, 2개의 reward functions의 차이가 어떤 x에 대한 함수 f(x)라면 두 reward function은 같다(같은 class이다)라고 정의를 한다.그리고 Lemma 1은, Plackett-Luce model framework에서 같은 class로 부터 나온 두 reward functions는 같은 preference distribution를 유도한다 이다. definition을 이용해서 lemma1을 증명하면,

 

 

 

plackett-luce model에 대한 preference distribution with reward function r' 이 있을 때(맨 윗줄), 정의에 의해 r' = r + f(x)로 표현할 수 있게 되고 이를 preference distribution 식에 대입하면, 두번째 줄처럼 전개가 되고, exp 성질에 의해 분모 분자의 $\exp(f(x))$는 소거가 될 수 있고, $\exp(f(x))$를 소거해보면 r'에 대한 preference prob은 r에 대한 preference prob 과 같은 것을 볼 수 있다.

 

 

 

그리고 lemma2는 같은 클래스로부터 나온 두개의 reward functions는 constrained RL problem에서 같은 optimal policy를 도출할 수 있다.

 

 

위에서 했던 것 처럼 r'에 대한 optimal policy $\pi_{r'}$을(맨 윗줄)에서 $r'(x,y)$를 $r'(x,y)=r(x,y)+f(x)$ 로 바꿔주면(두번째 줄), 마찬가지로 $\exp (\frac{1}{\beta} f(x))$를 소거할 수 있게 된다. 소거하고 보면 $\pi_{r}(y|x)$와 같음을 볼 수 있다.

 

 

 

 

그리고 definition, lemma를 통해 보인 이러한 mild assumptions에서 내릴 수 있는 Therorem은 Bradley-terry를 포함한 Plackett-Luce model과 같은 모든 reward class들은 policy와 reference policy의 ratio로 표현될 수 있다 는 것이다.

 

어떤 projection operator f를 reward에서 $\beta \log Z(x)$로 normalize 하는 것이라고 정의해보자. f에서 즉 수식 (8)에서, 두번째 텀은 오직 x에 관한 텀이기 때문에 앞에서 보인 assumption들로 인해 $f$는 $r(x,y)$와 같은 class라고 볼 수 있고, $r(x,y)$를 (4)번식 으로 대체하면, $f(r; \pi_{ref}, \beta)(x,y) = \beta \log \pi_r / \pi_{ref}$가 된다.

 

 

 

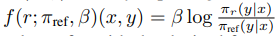
즉, projection operator f는 r(x,y)와 같은 클래스 라는 것이고, 그 말인 즉 슨 (8) 식에서 두번째 텀은 0이고 (8)식의 로그 뒤 텀인 (9) 식이 1이 된다는 것이다. 즉 $\pi(y|x)$는 모든 y에 대한 합이 1이고 양수이므로 valid distribution이며, (9)는 $r(x,y)$로부터 유도된 optimal policy의 partition function으로 볼 수 있다. 따라서 DPO의 키 인사이트는 표현가능한 reward model의 클래스를 보존하는 Plackett-Luce family 계열 선호모델에 특정 제약 조건을 부여할 수 있다는 것이다.

 

 

 

✲ Instability of Actor-Critic Algorithms

 

그리고 또 저자들은 PPO와 같은 standard actor-critic 알고리즘이 RLHF에 사용되면 왜 instable한지 얘기한다. 

 

 

 

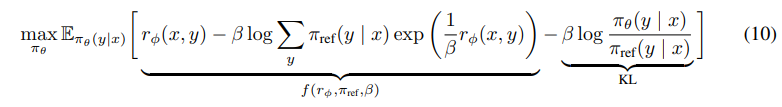
some algebra를 통해 optimization objecive를 도출하면 (10)식과 같이 되는데, 가운데의 $\beta \log$ ~ 부분은 baseline이 필요한 부분이고, DPO는 이 부분이 0이기 때문에 학습 불안정성을 야기하는 baseline을 필요로 하지 않는다고 주장한다.

 

 

✲ Experiment

 

 

 

 

 

---

 

 

‣ Review

 

DPO는 RLHF 파이프라인에서 Reward를 maximize하는 텀과 KL 패널티 텀에 Bradely-terry 모델을 reward로 치환하여 리워드 텀을 없애고 RLHF와 equivalent relative cross entropy 텀을 도출하였다. 이로 인해 리워드 모델이 필요한 부분을 우회가 가능하면서 선호 alignment tuning 과정에서 선호 리워드 개념을 내재적으로 사용할 수 있도록 했다.

Chatgpt로 RLHF에 대해 많은 연구와 관심이 이뤄지고 있지만 일반 개인이 reward model을 학습하거나 학습할만큼의 대량의 데이터를 확보하는 것은 아직 무리여 보인다. 또 데이터셋을 많이 수집하였다고 하더라도 reward model을 fitting하는 것도 어려울 뿐더러 reward model에 에러가 있다면 RL-tuning 단계까지 영향을 미칠 수도 있고 reward model 학습 후 RL 학습하는 것도 복잡하기 때문에 번거롭고 많은 작업이 생긴다. DPO는 이런 문제점을 해소해줄 수 있어 많은 관심을 받고 있는 것 같다. 학습 파이프라인도 훨씬 간결해지고 theoretical analysis도 잘 정리되어 있는 논문이었다.