[RL] Efficient Planning in a Compact Latent Action Space, TAP

Efficient Planning in a Compact Latent Action Space

 

Trajectory Transformer처럼 planning-based sequence modeling approach이며, Transformer의 느린 Decoding Time을 해결한 논문이다.

 

Sum up

1. state-conditioned VQ VAE를 trajectory를 모델링해서 compact latent space에서의 planning이 가능하게함
2. 생성모델의 prob estimation을 사용해서 explicitly하게 에이전트가 너무 behaviour policy를 벗어나거나 cofidence가 낮은 plan을 하지 않도록 함
3. offline RL setting에서 Empirical evaluation은 TAP가 효율적으로 high-dim continuous space에서 사용될 수 있고 기존 MB MF method를 능가하는 성능을 보여줌

Abstract

planning-based sequence modelling method는 continuous control 문제에서 좋은 결과를 보여주었지만(e.g. TT) 높은 complexity와 high-dim에서의 planning하는 것이 challenging하다. 그래서 TAP(Trajectory Autoencoding Planner)은 state를 conditioned하는 VQ-VAE(Vector Quantised Variational Autoencoder)를 사용해서 high state-action sequence를 scale한다. TAP는 현재 state가 주어졌을 때 trajectories의 conditional distributuion P(traj | s)를 모델링하며 step-by-step으로 planning(O(D^3) 하는 대신, optimal latent code sequence로 beam search를 하게 된다.(O(C))

 

Introduction

“Planning-based RL”은 MDP(Markov Decision Process)의 raw action space안에서 미리 정의되거나 learned dynamics model을 가지고 future trajectories를 rollout하게 된다. 이러한 planning procedure는 직관적이지만 raw action space 상에서 planning하는 것은 inefficient, inflexible하다. 특히 rollout할 dynamic model이 learned model인 경우, model을 정확하게 train하기는 어려우므로 해당 모델이 가진 error나 over-optimitic sampling을 planner가 exploit하게 되버린다. 또 raw action space 상에서 planning하는 것은 매우 느린 decision을 초래하므로 real-time control에 적용하기 어렵다.

그래서 해당 논문에서는 Trajectory Autoencoding Planner(TAP)를 제안하고, offline data에서 latent action model을 learning한 뒤, latent action variable로 future trajectory를 decoding하는 planner를 learning한다. latent action model을 잘 learning하면, 데이터셋 안의 그럴듯한 trajectories를 포착하게 되므로, out-of-distribution action을 막을 수 있는 효과도 있다.

• Model과 action space는 unsupervised manner로 learning 된 후
• 현재 state가 주어졌을 때, TAP의 encoder는 discrete latent code와 trajectories를 mapping하는 함수를 learning하고, decoder는 이에 대한 역 mapping 을 learning한다. 이 encoder와 decoder는 VQ-VAE(Vector Quantised Variational AutoEncoder)를 사용한다.

Figure 1

Figure 1(a)를 보면, latent code의 분포는 autoregressive Transformer로 모델링되고, Inference 시, action과 next state를 순차적으로 sampling하는 것 대신, TAP은 latent code를 sample하고(latent code를 autoregressive하게 sample한다.) Decoder를 통해 Trajectory를 구성한 다음, Trajectories 중 점수가 가장 높은 첫번째 action을 취한다. 따라서 VQ-VAE의 latent-code는 latent action이고, State-conditioned Decoder는 latent action을 decoding하게 된다.

TAP은 multiple transiton(여기서는 L=3)을 Single discrete latent로 mapping하므로 planning sequence 길이가 9였다면 3개의 latent code만 sample하게 되므로 decision delay가 크게 줄어든다. 게다가 하나의 latent code를 decoding한 뒤, plan하거나 다시 latent code를 sample하는 것이 아니라 모든 latent code를 다 sample하고 entire trajectory를 reconstructing하므로, step-by-step rollouts의 compound error를 완화하는데 도움이 된다고 저자들은 주장하고 있다.

 

 

Background

• VQ-VAE

VQ-VAE는 3개의 components를 가지고 있다. 1) input을 discrete latent code로 mapping하는 encoder, 2) latent code를 iput으로 reconstruct하는 decoder 3) latent variable의 learned prior distribution

encoder ouput, 즉 embedding vector x가 바로 decoder에 들어가게 되는 것이 아니고 codebook에 있는 vector로 query되어 들어가게 된다.

codebook $\mathbb{R}^{K\times D}, \$ K embedding vectors $e_k\in\mathbb{R}^D, \ k \in 1,2,3..K$

embedding vector x가 code book vector와 가장 가까운 code로 query되어 z가 되어 decoder의 input이 된다. $z_i=e_k,$ where $k=\argmin_j||x_i-e_j||_2$ . autoencoder는 $||x_i-e_j||_2, ||z_i-e_j||_2$ 이 두 거리를 최소화 하면서 reconstruction error를 최소화 하도록 training된다. 그리고 backpropogation때, gradient는 decoder의 output으로부터 encoder의 input에 직접적으로 copy된다.

(encoder와 decoder는 같이 training되긴 하지만 loss function은 따로 이기 때문에. backpropogation 중에 reconstruction loss의 gradient는 decoder output에 대해 계산되고, 이 gradient를 encoder input에 복사되서 encoder가 업데이터되어 decoder의 input을 재구성하는데 더 적합한 latent vector를 생성하도록 한다. gradient copy가 가능한 이유는 encoder, decoder가 함께 training되어 gradient를 공유할 수 있기 때문이다.)

 

 

Method

 

3. 1 Latent-Action Model and Planning

 

다음과 같이 trajectory tau가 있을때, sequence length는 T이다. 여기서 R_t는 Retun-to-go로, $R_t=\sum_{i=t}\gamma^{i-t}r_i$로, 앞으로 받을 return이다.

• Conditional distribution of the trajectory $p(\tau|s,z)=\mathbb{I}(\tau=h(s,z))p(z|s), \ z=(z_1, .. z_M)$ (s,z)는 trajectory tau로 deterministically mapping된다.
• z is latent action, p(z|s) is latenty policy
• latent-action model $h(s,z)=(s,z) \rightarrow \tau$

Deterministic MDP에서, p(z|s) >0인 임의의 h(s,z)에서 나온 trajectory tau는 실행가능한 trajectory, 즉 state s에서 시작해서 action sequence를 따라 trajectory를 복구할 수 있다. 따라서 latent action z를 최적화하여 최적의 planning을 찾을 수 있다.

 

저자들이 주장하기로는 latent code planning이 raw action planning보다 좋은 점은 크게 2가지가 있다고 한다.

1. latent-action model은 behavior policy를 support하는 action을 잡을 수 있다. 예를 들어서 X개의 policy가 섞여 있을 때, latent action space는, raw action space가 아무리 high demensionality하다고 해도, X개의 action들을 가지는 discrete space가 될 수 있다. 또한 in-distribution action만 허용하면 planner가 over-optimistic하기 쉬운 높은 uncertainty를 가지는 action을 쿼리하여 model의 약점을 악용하는 것을 방지할 수 있다.
2. latent-action model은 planning과 modeling간의 temporal structure를 분리할 수 있게 된다. raw action space에서 planning을 할 때 planning의 time resolution은 예측된 trajectory와 같아야 한다. 반면, latent action space에서 planning하는 것은 transition의 특정 step에 묶일 필요가 없어 훨씬 flexible하다. 이 속성을 이용하면 latent action sequence M의 길이를 planning horizon T보다 작게 되어서 효율적인 planning이 가능해진다.
3. 2 Learning a latent-action model with VQ-VAEs

하나의 transition $x_t:=(x_t,a_t,r_t,R_t)$를 하나의 토큰으로 보고 Transformer encoder, decoder를 learning하며, autoencoder와 prior over latent variable은 모두 first state s_1이 condition된다.

 

 

 

3. 2 Learning a latent-action model with VQ-VAEs

 

하나의 transition x_t:=(x_t,a_t,r_t,R_t)를 하나의 토큰으로 보고 Transformer encoder, decoder를 learning하며, autoencoder와 prior over latent variable은 모두 first state s_1이 condition된다.

Encoder Decoder

kernal, stride사이즈가 L인 1-dim max pooling layer로 Sequence T길이를 T/L 길이로 줄인다. 그리고 vector quantization을 통해 latent variable (z_1, .. z_M)을 얻고,

decoding할 때는 latent variable z를 L배 tiling(타일링, 늘림, torch interleave_repeat)한 후, embedding vector와 state를 concat하고 linear layer를 통과시킨 값에 positional embedding 값을 더하고, decoder의 input으로 넣어준다. decoder는 trajectory를 reconstrunction 하고 ($\hat{\tau}:=(\hat{x}_1,...\hat{x}_T))$ reconstruction과 실제 trajectory의 MSE를 계산해서 model을 업데이트한다.

 

Prior distribution of latent codes

VQ-VAE는 latent variable의 prior을 uniform이라고 가정하지만 실제로는 Prior를 train하는 것이 더 좋다고 한다. 그래서 TAP에서 prior p(z|s_1)을 학습하고 sample된 latent code를 다시 conditon으로 주는 autoregressive 방법을 사용한다. $p(z_t|z_{<t},s_1)=p(z_t|s_1,z_1,z_2..z_{t-1})$

latent-action model, prior model 모두 transformer를 사용했다.

 

 

3. 3 Planning in the discrete latent action space

 

Evaluation Criterion g:

initial state s_1과 prior에서 샘플된 latent z가 주어졌을 때, decoding 된 trajectories를 가지고 가장 좋은 trajectory를 판단하기 위한 creterion g는 위 수식과 같다.

Red Term은 예측된 Return-to-go의 score function이고 Bleu Term은 out-of-distribution의 penalty term이다. latent sequence의 prob이 threshold보다 크면, 높은 return을 가진 plan을 선택하도록 하고 알파는 discounted return의 가장 큰 값 보다 크게 설정되어, latent action sequence가 threshold보다 작으면 그럴듯한 trajectory를 선택하게 된다.

Inference time에 Sampling하는 방법은 prior distribution에서 sample하고 best return trajectory를 선택하도록 하는 “Vanila Sampling”이 있고 trajectory length가 짧을때 잘 작동한다. 또 다른 방법은 “Beam Search”를 하는 것이다. 처음 N개의 latent code로 NL길이의 trajectory를 디코딩하고 B개의 best Sequence만 유지하면서 새로운 code를 샘플한다. beam search도 마찬가지로 latent code로 searching하기 때문에 더 효율적이며 causal transformer 구조상 beam search를 하는 것이 성능에 좋다.

 

 

 

Experiments

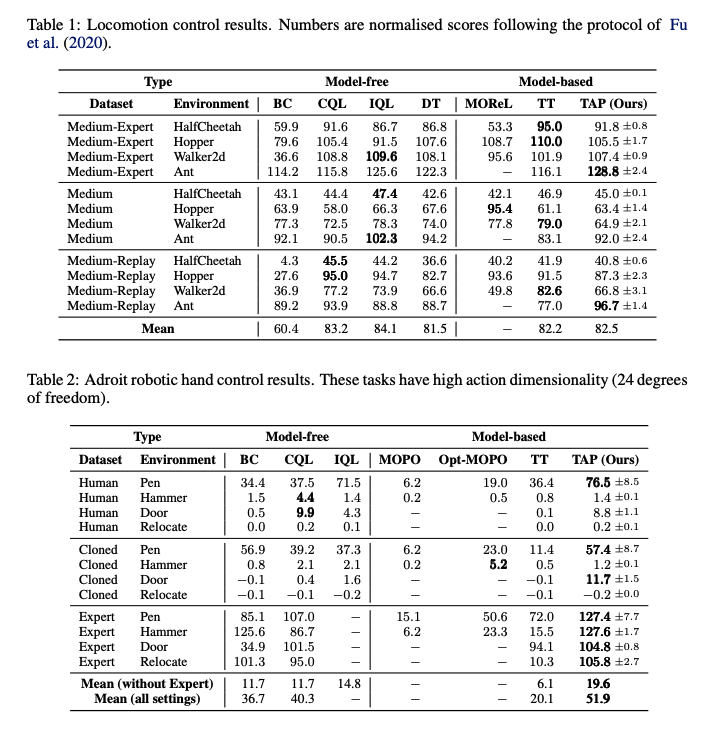
Locomotion control task에서 기존 Model free model들보다 성능이 많이 좋지는 않지만, Transformer 기반 모델을 사용할 때 Inference time을 temporal abstraction인 latent action space를 사용함으로써 많이 줄인 것이 키 포인트일 것 같다. 특히 action space가 커져도 inference time은 여전히 Linear하므로 실제 application에 적용하기 좋아보인다.

 

 

 

Paper Link

https://arxiv.org/pdf/2208.10291.pdf